Question
Question: (iii) $x^4 - 2x^2 - 63 \leq 0$...
(iii) x4−2x2−63≤0
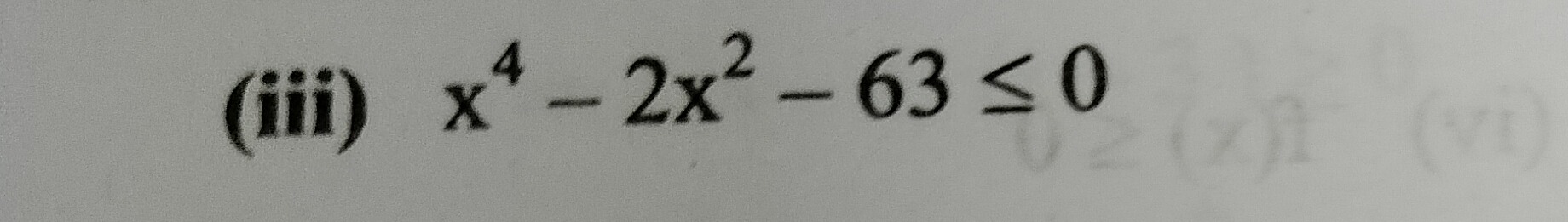
[-3, 3]
Solution
The given inequality is x4−2x2−63≤0. We can rewrite this inequality by treating it as a quadratic in terms of x2. Let y=x2. Since x is a real number, y=x2≥0. Substituting y into the inequality, we get: y2−2y−63≤0
Now, we solve this quadratic inequality for y. First, find the roots of the corresponding quadratic equation y2−2y−63=0. We can factor the quadratic expression: (y−9)(y+7)=0. The roots are y=9 and y=−7.
The quadratic expression (y−9)(y+7) represents a parabola opening upwards. It is less than or equal to zero between its roots. So, the inequality (y−9)(y+7)≤0 is satisfied when: −7≤y≤9
Now, substitute back y=x2: −7≤x2≤9
This compound inequality can be split into two separate inequalities:
- x2≥−7
- x2≤9
Let's analyze the first inequality, x2≥−7. For any real number x, its square x2 is always non-negative, i.e., x2≥0. Since 0≥−7, the inequality x2≥−7 is true for all real numbers x.
Now, let's analyze the second inequality, x2≤9. This inequality is satisfied when the absolute value of x is less than or equal to the square root of 9: ∣x∣≤9 which means ∣x∣≤3, so −3≤x≤3.
We need the values of x that satisfy both x2≥−7 and x2≤9. Since x2≥−7 is true for all real x, the solution set is determined solely by the inequality x2≤9. The solution to x2≤9 is −3≤x≤3.
Alternatively, after factoring the original expression directly: x4−2x2−63=(x2)2−2(x2)−63. This can be factored as a quadratic in x2: (x2−9)(x2+7)≤0
For any real number x, x2≥0, so x2+7≥7>0. The factor (x2+7) is always positive. For the product (x2−9)(x2+7) to be less than or equal to zero, the other factor (x2−9) must be less than or equal to zero: x2−9≤0, which means x2≤9. Taking the square root of both sides, we get ∣x∣≤3, which means −3≤x≤3.
The solution is the set of all real numbers x such that −3≤x≤3. In interval notation, this is [−3,3].
