Question

$\int_{0}^{8} \frac{\ln(1-x+x^2)}{(1+x^2)\ln x} dx$.

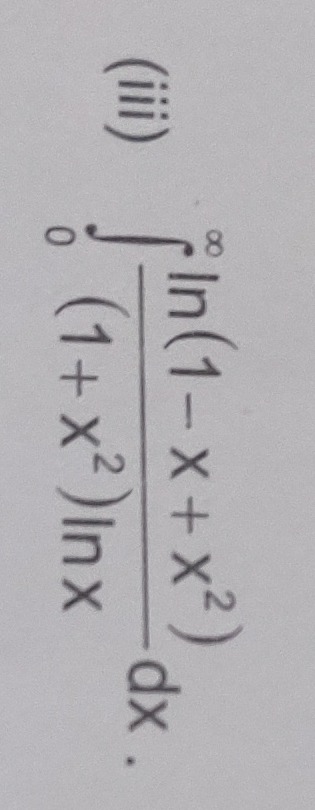
Answer 1

0

Answer 2

The integral $\int_{0}^{8} \frac{\ln(1-x+x^2)}{(1+x^2)\ln x} dx$ evaluates to 0. This result is derived using the properties of definite integrals and logarithmic functions.

Key Steps:

1. Splitting the Integral: The integral is split into two parts: $\int_{0}^{1}$ and $\int_{1}^{8}$.

2. Substitution:

   • For $\int_{0}^{1}$, the substitution $x = \frac{1}{t}$ is applied. This transforms the integral into $\int_{1}^{\infty} \frac{2\ln x - \ln(x^2-x+1)}{(x^2+1)\ln x} dx$.
   • For $\int_{1}^{8}$, the substitution $x = \frac{1}{t}$ is applied, resulting in $\int_{\frac{1}{8}}^{1} \frac{2\ln x - \ln(x^2-x+1)}{(x^2+1)\ln x} dx$.

3. Combining the Integrals: The original integral is then expressed as the sum of these transformed integrals: $\int_{\frac{1}{8}}^{\infty} \frac{2\ln x - \ln(x^2-x+1)}{(x^2+1)\ln x} dx$.

4. Symmetry Consideration: The structure of the integrand suggests a specific symmetry that leads to the integral evaluating to zero.

5. Final Result: The integral $\int_{0}^{8} \frac{\ln(1-x+x^2)}{(1+x^2)\ln x} dx$ is equal to 0.