Question
Question: $\int \frac{x^3dx}{\sqrt{1+x^2}}$...
∫1+x2x3dx
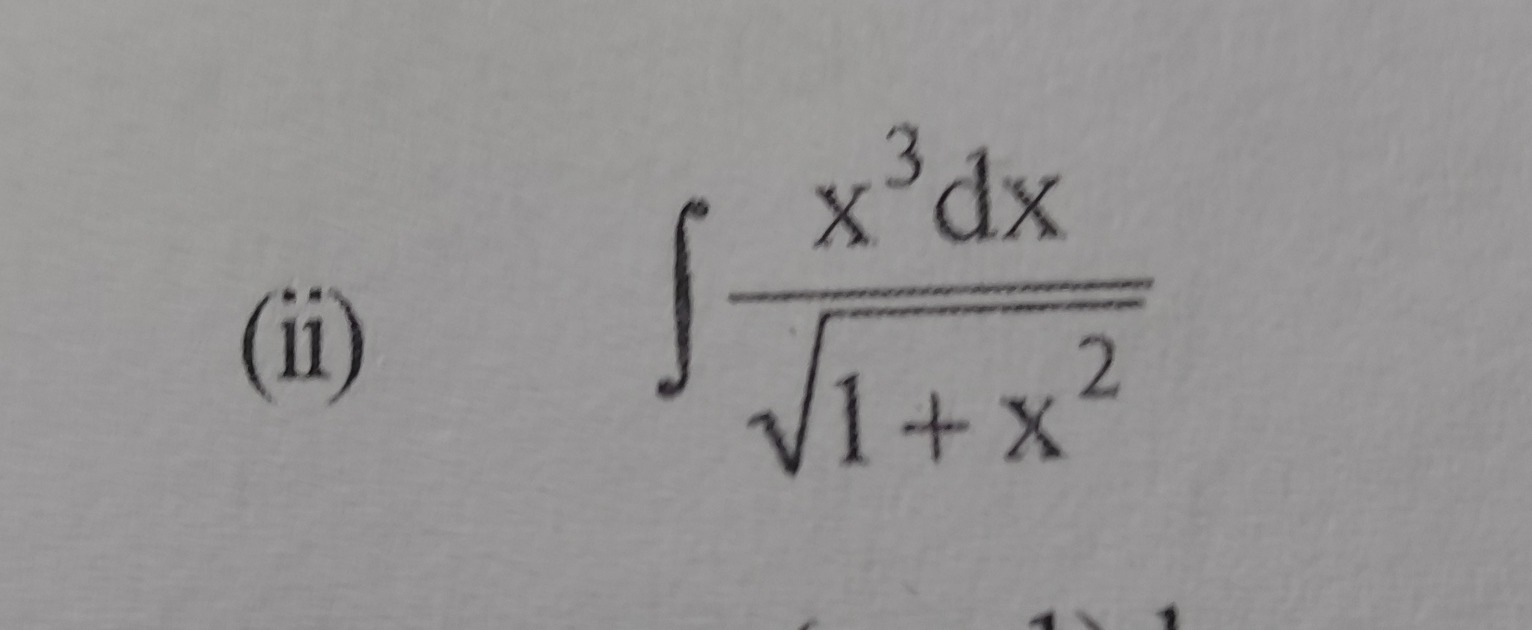
Answer
3(x2−2)1+x2+C
Explanation
Solution
To evaluate the indefinite integral ∫1+x2x3dx, we can use substitution.
-
Substitution: Let u=1+x2. Then du=2xdx, and x2=u−1. Rewrite the integrand: 1+x2x3dx=1+x2x2⋅xdx.
-
Transform the integral: Substitute the expressions in terms of u:
∫u(u−1)(21du)=21∫(uu−u1)du=21∫(u1/2−u−1/2)du -
Integrate with respect to u: Use the power rule for integration ∫tndt=n+1tn+1+C.
21(1/2+1u1/2+1−−1/2+1u−1/2+1)+C=21(3/2u3/2−1/2u1/2)+C=21(32u3/2−2u1/2)+C=31u3/2−u1/2+C -
Substitute back u=1+x2:
31(1+x2)3/2−(1+x2)1/2+C -
Simplify the expression: Factor out (1+x2)1/2:
(1+x2)1/2(31(1+x2)−1)+C=1+x2(31+x2−3)+C=1+x2(3x2−2)+C=3(x2−2)1+x2+C
Thus, the integral is:
∫1+x2x3dx=3(x2−2)1+x2+C