Question

$\frac{dy}{dx}=e^{x+y}+x^2e^{x^3+y}$

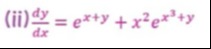
Answer 1

-e^{-y} = e^x + \frac{1}{3} e^{x^3} + C

Answer 2

The given differential equation is a first-order separable differential equation.

1. Rewrite the equation by factoring $e^y$: $\frac{dy}{dx} = e^y (e^x + x^2 e^{x^3})$.

2. Separate the variables by moving all terms involving $y$ to one side and all terms involving $x$ to the other side: $e^{-y} dy = (e^x + x^2 e^{x^3}) dx$.

3. Integrate both sides. The integral of $e^{-y}$ with respect to $y$ is $-e^{-y}$. The integral of $e^x$ with respect to $x$ is $e^x$. The integral of $x^2 e^{x^3}$ with respect to $x$ requires a substitution ($u=x^3$), resulting in $\frac{1}{3}e^{x^3}$.

4. Combine the integrated terms and add the constant of integration $C$ to obtain the general solution: $-e^{-y} = e^x + \frac{1}{3} e^{x^3} + C$.