Question
Question: $\begin{vmatrix}x+y+2z & x & y \\ z & y+z+2x & y \\ z & x & z+x+2y \end{vmatrix}=2(x+y+z)^3$...
x+y+2zzzxy+z+2xxyyz+x+2y=2(x+y+z)3
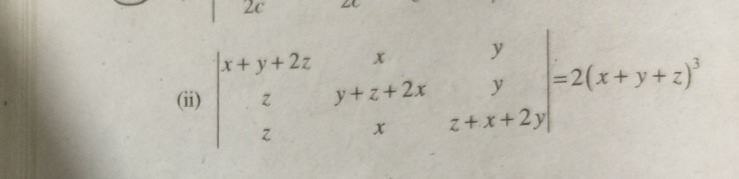
2(x+y+z)^3
Solution
To prove the identity: x+y+2zzzxy+z+2xxyyz+x+2y=2(x+y+z)3
Let the Left Hand Side (LHS) be Δ. Δ=x+y+2zzzxy+z+2xxyyz+x+2y
Step 1: Apply Column Operation Apply the column operation C1→C1+C2+C3. The elements of the new first column (C1′) will be:
- C11′=(x+y+2z)+x+y=2x+2y+2z=2(x+y+z)
- C21′=z+(y+z+2x)+y=2x+2y+2z=2(x+y+z)
- C31′=z+x+(z+x+2y)=2x+2y+2z=2(x+y+z)
The determinant becomes: Δ=2(x+y+z)2(x+y+z)2(x+y+z)xy+z+2xxyyz+x+2y
Step 2: Take out Common Factor Take out the common factor 2(x+y+z) from the first column (C1): Δ=2(x+y+z)111xy+z+2xxyyz+x+2y
Step 3: Apply Row Operations to Create Zeros Apply the following row operations to create zeros in the first column:
- R2→R2−R1
- R3→R3−R1
The determinant becomes: Δ=2(x+y+z)11−11−1x(y+z+2x)−xx−xyy−y(z+x+2y)−y Δ=2(x+y+z)100xx+y+z0y0x+y+z
Step 4: Evaluate the Determinant The resulting matrix is an upper triangular matrix. The determinant of a triangular matrix is the product of its diagonal elements. Δ=2(x+y+z)×[1×(x+y+z)×(x+y+z)] Δ=2(x+y+z)×(x+y+z)2 Δ=2(x+y+z)3
This is equal to the Right Hand Side (RHS) of the given identity. Hence, the identity is proved.
The final answer is 2(x+y+z)3
Explanation of the solution: The determinant is simplified by first applying the column operation C1→C1+C2+C3 to obtain a common factor 2(x+y+z) in the first column. This factor is then taken out. Subsequently, row operations R2→R2−R1 and R3→R3−R1 are performed to create zeros in the first column, leading to an upper triangular matrix. The determinant of this triangular matrix is the product of its diagonal elements, which simplifies to 2(x+y+z)3.
