Question
Question: If $|z_1|=1, |z_2|=2, |z_3|=3$ and $|9z_1\overline{z_2}+4z_1\overline{z_3}+z_2\overline{z_3}|=12$, t...
If ∣z1∣=1,∣z2∣=2,∣z3∣=3 and ∣9z1z2+4z1z3+z2z3∣=12, then find the value of ∣z1+z2+z3∣.
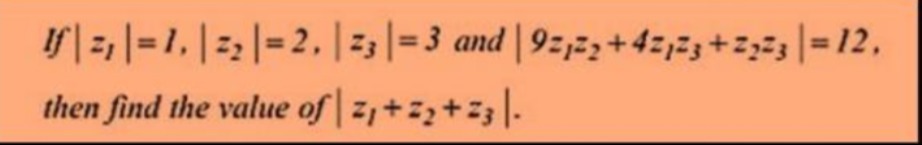
1
2
3
4
2
Solution
Let the given complex numbers be z1,z2,z3. We are given their magnitudes: ∣z1∣=1 ∣z2∣=2 ∣z3∣=3
From these, we have z1z1=∣z1∣2=1, z2z2=∣z2∣2=4, and z3z3=∣z3∣2=9. This implies z1=1/z1, z2=4/z2, and z3=9/z3.
We are also given the condition ∣9z1z2+4z1z3+z2z3∣=12. Let u=9z1z2, v=4z1z3, and w=z2z3. Let's find the magnitudes of these terms: ∣u∣=∣9z1z2∣=9∣z1∣∣z2∣=9×1×2=18. ∣v∣=∣4z1z3∣=4∣z1∣∣z3∣=4×1×3=12. ∣w∣=∣z2z3∣=∣z2∣∣z3∣=2×3=6.
The given condition is ∣u+v+w∣=12. We have magnitudes ∣u∣=18,∣v∣=12,∣w∣=6. For the sum of three complex numbers, ∣u+v+w∣≤∣u∣+∣v∣+∣w∣. 12≤18+12+6=36. This is true.
Consider the case where the complex numbers u,v,w are collinear. The value 12 can be obtained if u and w are in the same direction, and v is in the opposite direction, and their magnitudes add up as 18+6−12=12. This implies that u and w are in the same direction, and v is in the opposite direction. So, arg(u)=arg(w) and arg(v)=arg(u)+π.
From arg(u)=arg(w), we have u=kw for some k>0. ∣u∣=k∣w∣⟹18=k×6⟹k=3. So, u=3w. 9z1z2=3(z2z3) 3z1z2=z2z3.
From arg(v)=arg(u)+π, we have v=−mu for some m>0. ∣v∣=m∣u∣⟹12=m×18⟹m=12/18=2/3. So, v=−32u. 4z1z3=−32(9z1z2) 4z1z3=−6z1z2 Since z1=0, we can divide by z1: 4z3=−6z2. z3=−23z2. Taking conjugates, z3=−23z2.
Now we have two relations:
- 3z1z2=z2z3
- z3=−23z2
Substitute (2) into (1): 3z1z2=z2(−23z2) 3z1z2=z2(−23z2) 3z1z2=−23z2z2 3z1z2=−23∣z2∣2 3z1z2=−23(4) 3z1z2=−6 z1z2=−2.
Now we want to find ∣z1+z2+z3∣. Let S=z1+z2+z3. ∣S∣2=(z1+z2+z3)(z1+z2+z3) ∣S∣2=∣z1∣2+∣z2∣2+∣z3∣2+(z1z2+z2z1)+(z1z3+z3z1)+(z2z3+z3z2) ∣S∣2=∣z1∣2+∣z2∣2+∣z3∣2+2Re(z1z2)+2Re(z1z3)+2Re(z2z3).
We found z1z2=−2. So Re(z1z2)=−2. From z3=−23z2, we have z3=−23z2. z1z3=z1(−23z2)=−23(z1z2)=−23(−2)=3. So Re(z1z3)=3. z2z3=z2(−23z2)=−23z2z2=−23∣z2∣2=−23(4)=−6. So Re(z2z3)=−6.
Substitute these values into the expression for ∣S∣2: ∣S∣2=1+4+9+2(−2)+2(3)+2(−6) ∣S∣2=14−4+6−12 ∣S∣2=10+6−12 ∣S∣2=16−12 ∣S∣2=4.
Therefore, ∣S∣=∣z1+z2+z3∣=4=2.
