Question
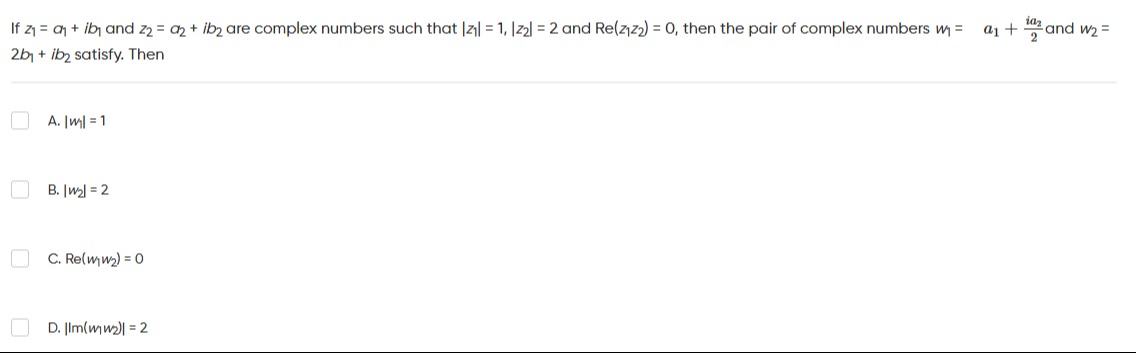
Question: If $z_1 = a_1 + ib_1$ and $z_2 = a_2 + ib_2$ are complex numbers such that $|z_1| = 1, |z_2| = 2$ an...
If z1=a1+ib1 and z2=a2+ib2 are complex numbers such that ∣z1∣=1,∣z2∣=2 and Re(z1z2)=0, then the pair of complex numbers w1=a1+2ia2 and w2=2b1+ib2 satisfy. Then
∣w1∣=1
∣w2∣=2
Re(w1w2)=0
∣Im(w1w2)∣=2
A, B, C
Solution
Let the given complex numbers be z1=a1+ib1 and z2=a2+ib2. We are given the following conditions:
- ∣z1∣=1⟹a12+b12=1⟹a12+b12=1 (Equation 1)
- ∣z2∣=2⟹a22+b22=2⟹a22+b22=4 (Equation 2)
- Re(z1z2)=0
First, calculate z1z2: z1z2=(a1+ib1)(a2−ib2)=a1a2−ia1b2+ib1a2−i2b1b2 z1z2=(a1a2+b1b2)+i(b1a2−a1b2)
Since Re(z1z2)=0, we have: a1a2+b1b2=0 (Equation 3)
From Equation 3, we can derive relations between a1,b1,a2,b2. If a2=0, then a1=−a2b1b2. Substitute this into Equation 1: (−a2b1b2)2+b12=1⟹a22b12b22+b12=1⟹b12(a22b22+1)=1 b12(a22b22+a22)=1. Using Equation 2 (a22+b22=4): b12(a224)=1⟹4b12=a22. This relation also holds if a2=0 (which implies b1=0). So, a22=4b12 (Relation A)
Similarly, if b2=0, then b1=−b2a1a2. Substitute this into Equation 1: a12+(−b2a1a2)2=1⟹a12+b22a12a22=1⟹a12(1+b22a22)=1 a12(b22b22+a22)=1. Using Equation 2 (a22+b22=4): a12(b224)=1⟹4a12=b22. This relation also holds if b2=0 (which implies a1=0). So, b22=4a12 (Relation B)
Now let's evaluate the options for w1=a1+2ia2 and w2=2b1+ib2.
A. ∣w1∣=1 ∣w1∣2=∣a1+2ia2∣2=a12+(2a2)2=a12+4a22. Using Relation A (a22=4b12): ∣w1∣2=a12+44b12=a12+b12. Using Equation 1 (a12+b12=1): ∣w1∣2=1⟹∣w1∣=1. So, Option A is true.
B. ∣w2∣=2 ∣w2∣2=∣2b1+ib2∣2=(2b1)2+b22=4b12+b22. Using Relation A (4b12=a22) and Relation B (b22=4a12): ∣w2∣2=a22+4a12. We also know from Equation 2 that a22+b22=4. And from Equation 1 that a12+b12=1. Substitute Relation A and Relation B into Equation 2: 4b12+4a12=4⟹4(b12+a12)=4⟹a12+b12=1, which is consistent with Equation 1. So, ∣w2∣2=4b12+b22=4b12+4a12=4(b12+a12)=4(1)=4. ∣w2∣2=4⟹∣w2∣=2. So, Option B is true.
C. Re(w1w2)=0 w1w2=(a1+2ia2)(2b1+ib2) w1w2=2a1b1+ia1b2+ia2b1−2a2b2 Re(w1w2)=2a1b1−2a2b2. We need to check if 2a1b1−2a2b2=0⟺4a1b1=a2b2. From Relation A, a2=±2b1. From Relation B, b2=±2a1. Substitute these into Equation 3: a1a2+b1b2=0. a1(±2b1)+b1(±2a1)=0. If a2=2b1 and b2=2a1: a1(2b1)+b1(2a1)=0⟹4a1b1=0. If a2=−2b1 and b2=−2a1: a1(−2b1)+b1(−2a1)=0⟹−4a1b1=0. In both these cases, a1b1=0, which implies a1=0 or b1=0. If a1=0, then b2=0 (from Relation B). If b1=0, then a2=0 (from Relation A). In these scenarios, a1b1=0 and a2b2=0, so 4a1b1=a2b2=0 holds. Thus Re(w1w2)=0.
Consider the other two cases for signs: If a2=2b1 and b2=−2a1: a1(2b1)+b1(−2a1)=0⟹2a1b1−2a1b1=0⟹0=0. This is always true. In this case, we need to check 4a1b1=a2b2. 4a1b1=(2b1)(−2a1)=−4a1b1. This implies 8a1b1=0, so a1b1=0. This means either a1=0 or b1=0. If a1=0, then b2=0 (from b2=−2a1). From Equation 1, b1=±1. From Equation 2, a2=±2. The condition a2=2b1 means a2 and b1 have the same sign. If b1=1,a2=2. Then a1=0,b1=1,a2=2,b2=0. Re(w1w2)=2(0)(1)−22(0)=0. If b1=−1,a2=−2. Then a1=0,b1=−1,a2=−2,b2=0. Re(w1w2)=2(0)(−1)−2(−2)(0)=0. So Re(w1w2)=0 holds.
If a2=−2b1 and b2=2a1: a1(−2b1)+b1(2a1)=0⟹−2a1b1+2a1b1=0⟹0=0. This is always true. In this case, we need to check 4a1b1=a2b2. 4a1b1=(−2b1)(2a1)=−4a1b1. This implies 8a1b1=0, so a1b1=0. Again, this means either a1=0 or b1=0. If a1=0, then b2=0 (from b2=2a1). From Equation 1, b1=±1. From Equation 2, a2=±2. The condition a2=−2b1 means a2 and b1 have opposite signs. If b1=1,a2=−2. Then a1=0,b1=1,a2=−2,b2=0. Re(w1w2)=2(0)(1)−2(−2)(0)=0. If b1=−1,a2=2. Then a1=0,b1=−1,a2=2,b2=0. Re(w1w2)=2(0)(−1)−22(0)=0. So Re(w1w2)=0 holds.
In all cases, Re(w1w2)=0. So, Option C is true.
D. ∣Im(w1w2)∣=2 From the calculation for Option C: w1w2=2a1b1−2a2b2+i(a1b2+a2b1). Since Re(w1w2)=0, the expression simplifies to w1w2=i(a1b2+a2b1). So, Im(w1w2)=a1b2+a2b1. We need to check if ∣a1b2+a2b1∣=2. Let's use the relations a2=±2b1 and b2=±2a1. We have four cases for the signs:
-
a2=2b1 and b2=2a1: Im(w1w2)=a1(2a1)+(2b1)b1=2a12+2b12=2(a12+b12). Using Equation 1 (a12+b12=1): Im(w1w2)=2(1)=2. ∣Im(w1w2)∣=∣2∣=2.
-
a2=−2b1 and b2=−2a1: Im(w1w2)=a1(−2a1)+(−2b1)b1=−2a12−2b12=−2(a12+b12). Using Equation 1 (a12+b12=1): Im(w1w2)=−2(1)=−2. ∣Im(w1w2)∣=∣−2∣=2.
-
a2=2b1 and b2=−2a1: Im(w1w2)=a1(−2a1)+(2b1)b1=−2a12+2b12=2(b12−a12). This value is not necessarily 2. For example, if a1=0,b1=1, then Im(w1w2)=2(1−0)=2. But if a1=1,b1=0, then Im(w1w2)=2(0−1)=−2. If a1=1/2,b1=1/2, then Im(w1w2)=2(1/2−1/2)=0. Since Im(w1w2) can be 0, ∣Im(w1w2)∣ is not always 2. For instance, if z1=21+i21, z2=0+i(2). Then a1=1/2,b1=1/2,a2=0,b2=2. ∣z1∣=1,∣z2∣=2. Re(z1z2)=Re((21+i21)(−2i))=Re(2−2i+22)=22=0. So this example does not satisfy all conditions.
Let's re-examine the consistency of the relations a2=2b1 and b2=−2a1 with a1a2+b1b2=0. a1(2b1)+b1(−2a1)=2a1b1−2a1b1=0. This is always consistent. Now, Im(w1w2)=a1b2+a2b1=a1(−2a1)+(2b1)b1=−2a12+2b12=2(b12−a12). We know a12+b12=1. So b12=1−a12. Im(w1w2)=2((1−a12)−a12)=2(1−2a12). The value of a12 can range from 0 to 1. If a12=0, Im(w1w2)=2(1)=2. If a12=1, Im(w1w2)=2(1−2)=−2. If a12=1/2, Im(w1w2)=2(1−1)=0. Therefore, ∣Im(w1w2)∣ is not always 2 in this case. It can be 0. For example, let a1=1/2,b1=1/2. Then z1=21+i21. Then a2=2b1=2, b2=−2a1=−2. z2=2−i2. Check conditions: ∣z1∣2=(1/2)2+(1/2)2=1/2+1/2=1. So ∣z1∣=1. ∣z2∣2=(2)2+(−2)2=2+2=4. So ∣z2∣=2. Re(z1z2)=Re((21+i21)(2+i2))=Re(21(2+i2)+2i(2+i2)) =Re(1+i+i−1)=Re(2i)=0. All conditions are satisfied. Now for w1 and w2: w1=a1+2ia2=21+i22=21+i21. w2=2b1+ib2=221+i(−2)=2−i2. w1w2=(21+i21)(2−i2)=(21+i21)2(1−i)=(1+i)(1−i)=1−i2=1+1=2. Here, Im(w1w2)=0. So ∣Im(w1w2)∣=0=2. Thus, Option D is not true.
The options that are true are A, B, and C.
