Question
Question: If \(z=x+iy\) and if the point P in the Argand Plane represents z, then describe geometrically the l...
If z=x+iy and if the point P in the Argand Plane represents z, then describe geometrically the locus of z satisfying equations,
(i)∣z−2−3i∣=5(ii)2∣z−2∣=∣z−1∣
Solution
This question involves the concept of complex number. In this question, we have to put z=x+iy and solve using the concepts like, z=∣z∣=x2+y2. So, if any complex number is in form of z=α+iβ, then modulus of ∣z∣=α2+β2.
Complete step-by-step answer:
Now, we will consider the first equation, that is,
∣z−2−3i∣=5
We have been given in the question that z=x+iy, so on substituting this value of z in the above equation, we will get,
∣x+iy−2−3i∣=5
On writing the real and the imaginary parts separately, we get,
∣(x−2)+i(y−3)∣=5
Now, let α be a complex number which is equal to (x−2)+(y−3)i. So, we will get the modulus of α as,
∣α∣=(x−2)2+(y−3)2
So, we can write,
(x−2)2+(y−3)2=5
On squaring the above equation, we get,
(x−2)2+(y−3)2=25
Now, we know that (x−α)2+(y−β)2=r2 is the equation of a circle with the center (α,β) and the radius r.
So, on comparing our equation with the equation of the circle, we get to know that,
(x−2)2+(y−3)2=25 is the equation of a circle with the center (2,3) and the radius 5.
So, the locus of z in the equation ∣z−2−3i∣=5 is circle with the center (2,3) and the radius 5.
Now, we will consider the second equation, that is,
2∣z−2∣=∣z−1∣
We have been given in the question that, z=x+iy, so on substituting this value of z in the above equation, we will get,
2∣x+iy−2∣=∣x+iy−1∣
On writing the real and the imaginary parts separately, we get,
2∣(x−2)+iy∣=∣(x−1)+iy∣
On solving the modulus on both the sides, we get,
2(x−2)2+y2=(x−1)2+y2
On taking the square root on both the sides of the above equation, we get,
4[(x−2)2+y2]=(x−1)2+y2
We know that (a−b)2=a2+b2−2ab, so on applying this property in the above equation, we get,
4[x2+4−4x+y2]=x2+1−2x+y2
On solving it further, we get,
4x2+16−16x+4y2=x2+1−2x+y2
On taking all the terms to one side, we get,
4x2−x2−16x+2x+4y2−y2+16−1=03x2+3y2−14x+15=0
On dividing the whole equation by 3, we get,
x2+y2−314x+5=0
By making perfect squares, we get,
(x−37)2+y2+5−949=0(x−37)2+y2−94=0(x−37)2+y2=(32)2
Now, we know that the equation of a circle with the center (α,β) and the radius r is (x−α)2+(y−β)2=r2.
So, on comparing both the equations, we get to know that,
(x−37)2+y2=(32)2 is the equation of a circle with the center (37,0) and the radius 32.
So, the locus of z in equation 2∣z−2∣=∣z−1∣ is also a circle.
Note: In equation (i), that is ∣z−2−3i∣=5. We get,
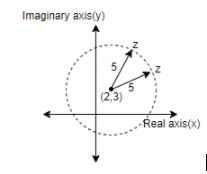
If we assume a complex number α=2+3i, then (z−α) is also a complex number and ∣z−α∣ is the distance between z and α, that is 5. So, whatever is z, the distance between z and a constant point, α is constant. So, this represents a circle.
So, ∣z−α∣=r represents a circle with the center α and radius r.
In equation (ii), that is 2∣z−2∣=∣z−1∣, we can also write it as ∣z−1∣∣z−2∣=21.
And, we know that in ∣z−β∣∣z−α∣=qp, locus of z is a circle with diameter endpoints, internal and external division of α and β in the ratio p:q.
So, ∣z−1∣∣z−2∣=21 is a circle with the diametric end point A and B.
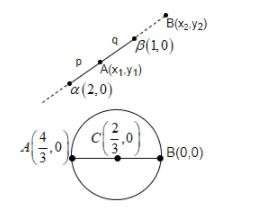
x1=32+2=34,y1=30+0=0x2=32−2=0,y2=30−0=0
