Question
Question: If z is a unimodular complex number such that Re(z - 1) + Re($z^2$) = $\int_{0}^{\pi/2}$ sin x ln | ...
If z is a unimodular complex number such that Re(z - 1) + Re(z2) = ∫0π/2 sin x ln | sin x - cos x | dx, then z can satisfy
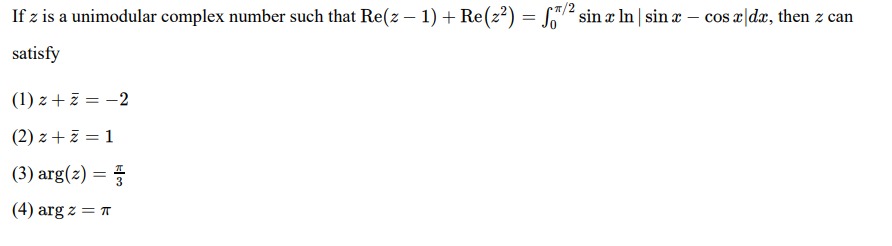
z + zˉ = -2
z + zˉ = 1
arg(z) = 3π
arg z = π
(1), (2), (3), (4)
Solution
The problem requires us to find which conditions a unimodular complex number z can satisfy, given an equation involving its real part and an integral.
1. Evaluate the integral: Let the given integral be I. I=∫0π/2sinxln∣sinx−cosx∣dx
Using the property ∫abf(x)dx=∫abf(a+b−x)dx: I=∫0π/2sin(π/2−x)ln∣sin(π/2−x)−cos(π/2−x)∣dx I=∫0π/2cosxln∣cosx−sinx∣dx
Since ∣A∣=∣−A∣, we have ∣cosx−sinx∣=∣sinx−cosx∣. So, I=∫0π/2cosxln∣sinx−cosx∣dx.
Adding the two expressions for I: 2I=∫0π/2(sinx+cosx)ln∣sinx−cosx∣dx. Let u=sinx−cosx. Then du=(cosx+sinx)dx. When x=0, u=sin0−cos0=0−1=−1. When x=π/2, u=sin(π/2)−cos(π/2)=1−0=1.
Substituting these into the integral: 2I=∫−11ln∣u∣du. Since ln∣u∣ is an even function, ∫−11ln∣u∣du=2∫01lnudu. We know that ∫lnudu=ulnu−u. So, 2I=2[ulnu−u]01=2[(1ln1−1)−limu→0+(ulnu−u)]. As ln1=0 and limu→0+ulnu=0: 2I=2[(0−1)−(0−0)]=2(−1)=−2. Therefore, I=−1.
2. Simplify the Left Hand Side (LHS): Given that z is a unimodular complex number, its modulus is 1, i.e., ∣z∣=1. Let z=x+iy, where x,y∈R. From ∣z∣=1, we have x2+y2=1.
Re(z - 1) = Re((x - 1) + iy) = x−1. z2=(x+iy)2=x2−y2+2ixy. Re(z2) = x2−y2. Substitute y2=1−x2 (from x2+y2=1): Re(z2) = x2−(1−x2)=x2−1+x2=2x2−1.
Now, substitute these back into the LHS: LHS = Re(z - 1) + Re(z2) = (x−1)+(2x2−1)=2x2+x−2.
3. Equate LHS and RHS: We have LHS = 2x2+x−2 and RHS = −1. 2x2+x−2=−1 2x2+x−1=0. This is a quadratic equation in x. We can factor it: (2x−1)(x+1)=0. This gives two possible values for x=Re(z): x=1/2 or x=−1.
4. Check the options based on possible values of x: Recall that for a complex number z=x+iy with ∣z∣=1, x=cos(arg(z)). Also, z+zˉ=(x+iy)+(x−iy)=2x.
Case 1: x=1/2 If x=1/2, then z+zˉ=2(1/2)=1. This matches option (2). To find y, use y2=1−x2: y2=1−(1/2)2=1−1/4=3/4. So, y=±3/2. The possible values for z are z=1/2+i3/2 or z=1/2−i3/2. If z=1/2+i3/2, then z=eiπ/3. So, arg(z)=π/3. This matches option (3). If z=1/2−i3/2, then z=e−iπ/3. So, arg(z)=−π/3 (or 5π/3).
Case 2: x=−1 If x=−1, then z+zˉ=2(−1)=−2. This matches option (1). To find y, use y2=1−x2: y2=1−(−1)2=1−1=0. So, y=0. The only possible value for z is z=−1+i(0)=−1. If z=−1, then z=eiπ. So, arg(z)=π. This matches option (4).
Since the question asks "z can satisfy", it means any condition that holds for at least one valid z is a correct option. We have found that:
- z+zˉ=−2 is satisfied by z=−1.
- z+zˉ=1 is satisfied by z=1/2+i3/2 (or z=1/2−i3/2).
- arg(z)=π/3 is satisfied by z=1/2+i3/2.
- arg(z)=π is satisfied by z=−1.
Therefore, all the given options are conditions that z can satisfy.
