Question

If z is a complex number which simultaneously satisfies the equations $3|z - 12| = 5|z - 8i|$ and $|z - 4| = |z - 8|$, then Im(z) can be

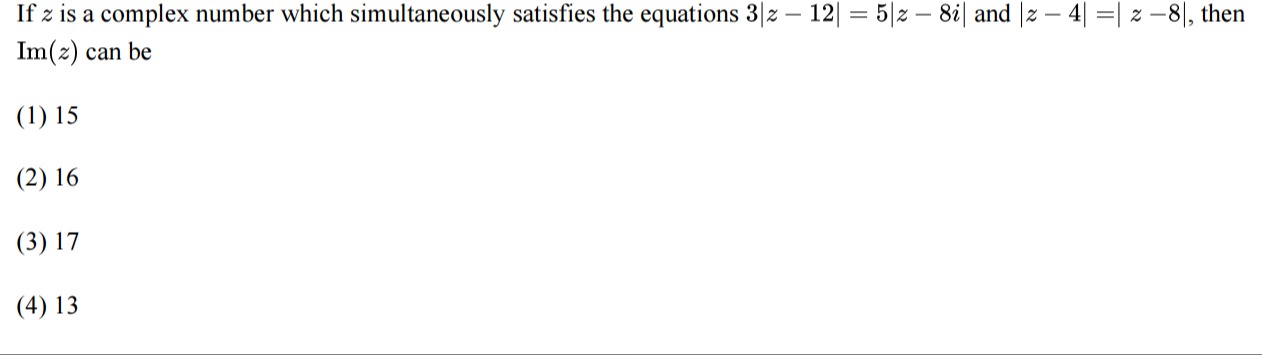
• A. 15
• B. 16
• C. 17
• D. 13

Answer 1

Answer: (C)

17

Answer 2

Let $z = x + iy$.

1. From the equation

   $$|z-4| = |z-8|$$

   we have

   $$\sqrt{(x-4)^2+y^2} = \sqrt{(x-8)^2+y^2}.$$

   Squaring both sides:

   $$(x-4)^2 = (x-8)^2.$$

   Expanding and simplifying:

   $$x^2 - 8x + 16 = x^2 - 16x + 64 \quad \Rightarrow \quad 8x = 48 \quad \Rightarrow \quad x = 6.$$

2. Now substitute $x = 6$ into

   $$3|z-12| = 5|z-8i|$$

   where $z = 6 + iy$.

   Compute the moduli:

   $$|z - 12| = |6 + iy - 12| = |-6 + iy| = \sqrt{(-6)^2 + y^2} = \sqrt{36+y^2},$$ $$|z - 8i| = |6 + iy - 8i| = |6 + i(y-8)| = \sqrt{6^2 + (y-8)^2} = \sqrt{36+(y-8)^2}.$$

   So the equation becomes:

   $$3\sqrt{36+y^2} = 5\sqrt{36+(y-8)^2}.$$

   Squaring both sides:

   $$9(36+y^2)= 25[36+(y-8)^2].$$

   Expand $(y-8)^2$:

   $$9(36+y^2) = 25(36+y^2-16y+64).$$

   Simplify:

   $$324+9y^2 = 25y^2 - 400y + 2500.$$

   Rearranging:

   $$16y^2 - 400y + 2176 = 0.$$

   Dividing by 16:

   $$y^2 - 25y + 136 = 0.$$

   Factorizing/discriminant method:

   $$y = \frac{25 \pm \sqrt{625-544}}{2} = \frac{25 \pm \sqrt{81}}{2} = \frac{25 \pm 9}{2}.$$

   Hence,

   $$y = 17 \quad \text{or} \quad y = 8.$$

Given the options $(1)\ 15$, $(2)\ 16$, $(3)\ 17$, $(4)\ 13$, the valid value is $y = 17$.