Question

If z is a complex number satisfying the equation$\left| {z + i} \right| + \left| {z - i} \right| = 8$, on the complex plane then maximum value of $\left| z \right|$ is
A.2
B.4
C.6
D.8

Answer 1

Hint : Complex number is a number generally represented as $z = a + ib$, where $a$ and $b$ is real number represented on real axis whereas $i$ is an imaginary unit represented on imaginary axis whose value is $i = \sqrt { - 1}$. Modulus of a complex number is length of line segment on real and imaginary axis generally denoted by $\left| z \right|$ whereas angle subtended by line segment on real axis is argument of matrix denoted by argument (z) calculated by trigonometric value. Argument of complex numbers is denoted by $\arg (z) = \theta = {\tan ^{ - 1}}\dfrac{b}{a}$.

Complete step-by-step answer :
In this question, we need to determine the maximum value of $\left| z \right|$ such that $\left| {z + i} \right| + \left| {z - i} \right| = 8$ have to be satisfied. For this we will use the properties of the complex numbers as discussed above.
$\left| {z + i} \right| + \left| {z - i} \right| = 8 - - (i)$
This equation can be written as
$\left| {z - \left( { - i} \right)} \right| + \left| {z - i} \right| = 8 - - (ii)$
We know imaginary unit $i$is represented on a plane as

Now it is given that a point z is on the plane whose sum of distance from points $i$ and $- i$ is given as 8 as shown in the diagram below

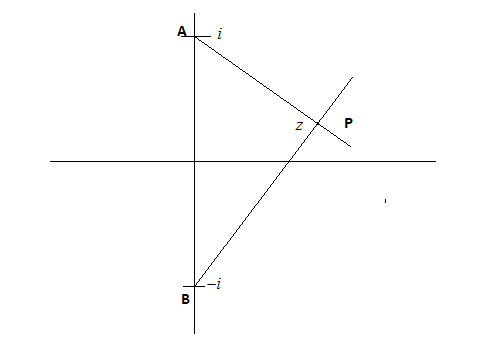
We know the equation of the locus from point P for the sum of distance between two fixed points is constant $PA + PB = 2a - - (iii)$and this constant form an ellipse

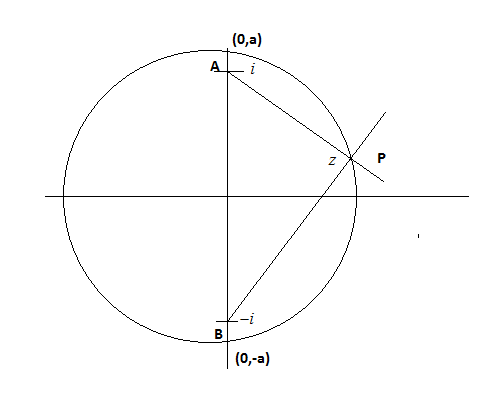
Now if we compare equation (iii) with the equation (i), we can say

$$2a = 8 \\\ a = 4 \\\$$

Where $a = 4$ is the maximum value from which the ellipse pass, hence we can say the maximum value of $\left| z \right|$ is $= 4$

Note : Complex numbers are always written in the form of $z = a + ib$ where $a$ and $b$ are real numbers whereas $i$being imaginary part. We can convert a degree into radian by multiplying it by $\dfrac{\pi }{{180}}$. Argument of complex numbers is denoted by $\arg (z) = \theta = {\tan ^{ - 1}}\dfrac{b}{a}$.