Question

If $z = \frac{1+i\sqrt{3}}{2i\left(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3}\right)}$ then find $|z| \text{ \& } \text{amp}(z)$

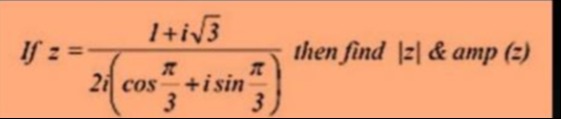
Answer 1

$|z| = 1$ and $\text{amp}(z) = -\frac{\pi}{2}$

Answer 2

1. Convert numerator $1+i\sqrt{3}$ to polar form: modulus $2$, argument $\frac{\pi}{3}$.
2. Convert denominator $2i(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3})$ to polar form: $2i$ has modulus $2$ and argument $\frac{\pi}{2}$. $(\cos\frac{\pi}{3}+i\sin\frac{\pi}{3})$ has modulus $1$ and argument $\frac{\pi}{3}$. The product has modulus $2 \times 1 = 2$ and argument $\frac{\pi}{2} + \frac{\pi}{3} = \frac{5\pi}{6}$.
3. For $z = \frac{N}{D}$, $|z| = \frac{|N|}{|D|} = \frac{2}{2} = 1$.
4. $\text{amp}(z) = \arg(N) - \arg(D) = \frac{\pi}{3} - \frac{5\pi}{6} = -\frac{\pi}{2}$.