Solveeit Logo
Login

Question

Question: If \({Z_1}\) and \({Z_2}\) are lying on \(|Z - 3|\,\,\, = 4\) and \(|Z - 1| + |Z + 1| = 3\) respecti...

If Z1{Z_1} and Z2{Z_2} are lying on ∣Z−3∣   =4|Z - 3|\,\,\, = 4 and ∣Z−1∣+∣Z+1∣=3|Z - 1| + |Z + 1| = 3 respectively then the range of ∣Z1−Z2∣ |{Z_1} - {Z_2}|\, is
A) [0,∞\infty )
B) [0,1]
C) [0,17/2]
D) [0,3/2]

Explanation

Solution

We know that the equation of circle with center A(a,0) and radius r is ∣Z−A∣=r|Z - A| = r
We also know that the equation of ellipse with foci C(c,0) and D(d,0) and with length of major axis as a ‘l’ is ∣Z−C∣+∣Z−D∣=l|Z - C| + |Z - D| = l
So the given equations are the equations of circle and ellipse. Draw a graph including both circle and ellipse and find the maximum and minimum distances.

Complete step by step answer:
If we draw the graph of given equations it will as the figure shown below.

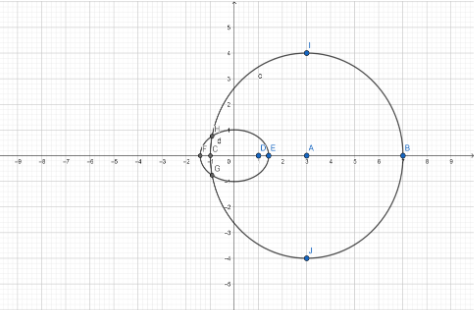
By comparing the equation of the circle with the given equation we got to know that the center (A) is (3,0) and radius r is 4.
By comparing the equation of the ellipse with the given equation we got to know that the foci are C(-1,0) .
and D(1,0) and the length of the major axis FE is 3.
We know that CF=DE and CD=distance between (-1,0) and (1,0)=2
Length of major axis =FC+CD+DE=2FC+2
=>3=2FC+2
=>FC=1/2=DE
As FC and DE are 1/2,
F=(-3/2,0) ;
E=(3/2,0);
Now they have asked the value of ∣Z1−Z2∣|{Z_1} - {Z_2}| where Z1{Z_1} and Z2{Z_2} are points on circle and ellipse respectively.
We know that distance is always a positive value. By looking at the graph we can easily say that if Z1{Z_1} = Z2{Z_2} = H or G then the value of ∣Z1−Z2∣|{Z_1} - {Z_2}| will be Zero. So the minimum value of ∣Z1−Z2∣|{Z_1} - {Z_2}| is 0.
Now coming to the maximum value, Z2{Z_2} will be obviously F and from F we need to find maximum distance to the circle.
We know a property of a circle that the distance from an outside point to a circle will be maximum when the distance line passes through the centre, Which says the distance will be maximum when Z1=B{{Z_1}=B}.
Therefore the maximum distance is FB= FC+CB= FC+2r= 12+8=172\dfrac{1}{2} + 8 = \dfrac{{17}}{2}
Therefore the range will be [0,17/2].

The correct option is C.

Note:
In this problem all the numericals are almost integral values or easily solved, but not all the questions will be so. So, practice by taking other values and drawing graphs for those questions. In almost many problems you get the solutions by drawing graphs, so practice drawing graphs frequently.