Question

If Young’s double slit experiment of light, interference is performed in water, which one of the following is correct?
A. Fringe width will decrease
B. Fringe width will increase
C. There will be no fringe
D. Fringe width will remain unchanged

Answer 1

The question is asking about the condition of fringe width under water. We must think about the formula of fringe width, which is related to wavelength. Also, wavelength has a relationship with refractive index i.e. $n=\dfrac{{{\lambda }_{air}}}{{{\lambda }_{medium}}}$. Using these relations, we will conclude the change in fringe width.

Formula Used:
Fringe width for interference condition:
$\beta =\dfrac{\lambda D}{d}$
Where, $\beta$ is the Fringe width.
$\lambda$ is the wavelength of coherent light.
$D$ is the distance between source and screen.
$d$ distance between two slits.

Complete answer:
We know that in Young’s Double Slit Experiment, the interference obtained on the screen has the consecutive bright and dark fringes. The separation between these bright and dark fringes is called fringe width. We will use the diagram of YDSE for better understanding.

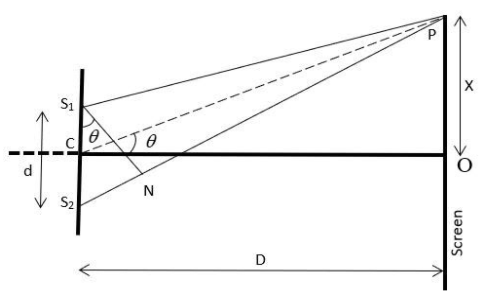
Fringe width is given by:
$\beta =\dfrac{\lambda D}{d}$
But in our question Young’s double slit experiment is performing under water.
And we know that water has a refractive index higher than that of air.
Refractive index: The ratio of speed of light in one medium with respect to another medium. In general the first medium is air. Refractive Index of air is 1. Medium other than air has a refractive index greater than one.
Refractive Index is a unit less quantity and generally represented by $n$ .

& n=\dfrac{{{v}_{air}}}{{{v}_{medium}}} \\\ & n=\dfrac{{{\lambda }_{air}}}{{{\lambda }_{medium}}} \\\ & {{\lambda }_{medium}}=\dfrac{{{\lambda }_{air}}}{n} \\\ \end{aligned}$$ Hence wavelength in the medium other than air will decrease. Also, $$\beta =\dfrac{\lambda D}{d}$$ . Here, distance between the slit and screen $$(D)$$ and distance between two slits $$(d)$$ remains unchanged under water. Therefore, $$\beta \propto \lambda $$ $$\begin{aligned} & {{\beta }_{medium}}\propto {{\lambda }_{medium}} \\\ & {{\beta }_{medium}}=\dfrac{{{\lambda }_{air}}}{n} \\\ & {{\beta }_{medium}}=\dfrac{{{\beta }_{air}}}{n} \\\ \end{aligned}$$ It is clear from the above equation, Fringe width will decrease when we perform Young’s Double Slit Experiment under water. **Hence, the correct answer is option a.** **Note:** Student must remember: 1) Frequency of light will never change when light enters from one medium to another it’s the wavelength and velocity of light which varies. 2) Refractive index of air or vacuum is one. Therefore the light has its maximum speed in air or vacuum. 3) Refractive index of water is close to 1.33.