Question

If you can change location of the point A on the wall and hence the orientation of the string OA without altering the orientation of the string OB as shown in figure -II. What angle should the string OA make with the wall so that a minimum tension is developed in it?

Answer 1

In this question, as the suspended object is in equilibrium, then all the forces acting on it is balanced. We need to equate both the horizontal and the vertical components of the forces working on the body, then simultaneously solving those equations will give us our desired result.

Complete step by step answer:
From the given diagram, we get that all the forces are balanced;

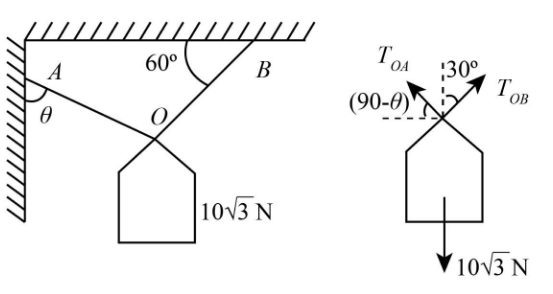
Let us consider the tension acting on the string OA is ${T_{OA}}$ , and the tension working on the string OB is ${T_{OB}}$.
Equating the horizontal forces acting on the junction point;

\;\;\;\;{T_{OA}}\sin \theta = {T_{OB}}\cos {\rm{ 6}}{{\rm{0}}^ \circ }\\\ \Rightarrow {T_{OA}}\sin \theta = {T_{OB}} \times \dfrac{1}{2}\\\ \Rightarrow {T_{OB}} = 2{T_{OA}}\sin \theta \end{array}$$ ……(i) Equating the vertical forces acting on the junction point; $${T_{OA}}\cos \theta + {T_{OB}}\sin \;{60^ \circ } = 10\sqrt 3 $$ ……(ii) Substituting the value obtained from expression (i) in expression (ii), we have; $$\begin{array}{l} {\rm{ }}{T_{OA}}\cos \theta + 2{T_{OA}}\sin \theta \times \dfrac{{\sqrt 3 }}{2} = 10\sqrt 3 \\\ \Rightarrow {T_{OA}}\left( {\cos \theta + \sqrt 3 \sin \theta } \right) = 10\sqrt 3 \\\ \Rightarrow {T_{OA}} = \dfrac{{10\sqrt 3 }}{{\cos \theta + \sqrt 3 \sin \theta }} \end{array}$$ ……(iii) For the value of tension in string OA to be minimum, the denominator in expression (iii) must have the maximum possible value. On analyzing the value of the denominator for all the possible values of $$\theta $$ we have; Let,$$f(\theta ) = \cos \theta + \sqrt 3 \sin \theta $$ Now, $$\begin{array}{c} f'(\theta ) = - \sin \theta + \sqrt 3 \cos \theta \\\ = \sqrt 3 \cos \theta - \sin \theta \end{array}$$ To find the saddle point we substitute $$f'(\theta ) = 0$$, then we get; $$\begin{array}{c} \;\;\;\sqrt 3 \cos \theta - \sin \theta = 0\\\ {\rm{or,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\sin \theta = \sqrt 3 \cos \theta \\\ {\rm{or,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\dfrac{{\sin \theta }}{{\cos \theta }} = \sqrt 3 \\\ {\rm{or, }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{tan}}\theta = \sqrt 3 \\\ {\rm{or,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tan \theta = 1.732\\\ {\rm{or,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\tan \theta = \tan {\left( {60} \right)^ \circ }\\\ {\rm{or,}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\theta = {60^ \circ } \end{array}$$ Differentiating $$f'\left( \theta \right)$$ again, we get; $$f''\left( \theta \right) = - \left( {\sqrt 3 \sin \theta + \cos \theta } \right)$$ Substituting $$\theta = {60^ \circ }$$in the above equation we get; $$\begin{array}{c} f''({60^ \circ }) = - (\sqrt 3 \sin {60^ \circ } + \cos {60^ \circ })\\\ = - \left( {\dfrac{3}{2} + \dfrac{1}{2}} \right)\\\ = - 2 \end{array}$$ So, $$f({60^ \circ }) = \sqrt 3 \sin {60^ \circ } + \cos {60^ \circ } = \dfrac{3}{2} + \dfrac{1}{2} = 2$$ , is the point of maxima. Hence, the term $$\cos \theta + \sqrt 3 \sin \theta $$ attains a maximum value of 2 at an angle, $$\theta $$= $${60^ \circ }$$and the value of tension at this angle will be minimum. Therefore, the string should make an angle of $${60^ \circ }$$with the wall to develop minimum tension. **Additional Information:** Any extra force unbalanced force will throw the system out of equilibrium. **Note:** In the current question, we take into consideration that in the process of changing the angle is made very slowly so that no added external force is included in the system, as such external force might disrupt the equilibrium of the system. The condition of equilibrium must be maintained through the entire process for the above expressions to be applicable.