Question
Question: If $y^{1/4} + y^{-1/4} = 2x$, and $(x^2 - 1)\frac{d^2y}{dx^2} + \alpha x \frac{dy}{dx} + \beta y = 0...
If y1/4+y−1/4=2x, and (x2−1)dx2d2y+αxdxdy+βy=0, then ∣α−β∣ is equal to ____.
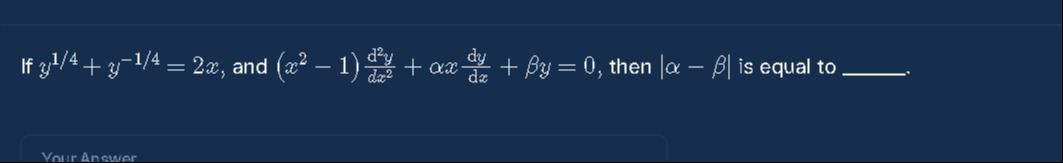
17
Solution
Let t=y1/4. Then y=t4. The given equation y1/4+y−1/4=2x becomes t+t1=2x. Differentiating t+t1=2x with respect to x: dxdt−t21dxdt=2 dxdt(1−t21)=2 dxdt(t2t2−1)=2 dxdt=t2−12t2.
Now we find the derivatives of y with respect to x: dxdy=dtdydxdt=4t3⋅t2−12t2=t2−18t5.
Differentiating dxdy with respect to x: dx2d2y=dxd(t2−18t5)=dtd(t2−18t5)dxdt dtd(t2−18t5)=8(t2−1)25t4(t2−1)−t5(2t)=8(t2−1)25t6−5t4−2t6=8(t2−1)23t6−5t4=(t2−1)28t4(3t2−5). So, dx2d2y=(t2−1)28t4(3t2−5)⋅t2−12t2=(t2−1)316t6(3t2−5).
From t+t1=2x, we have x=2tt2+1. Then x2−1=(2tt2+1)2−1=4t2(t2+1)2−4t2=4t2t4+2t2+1−4t2=4t2t4−2t2+1=4t2(t2−1)2.
Substitute these into the given differential equation (x2−1)dx2d2y+αxdxdy+βy=0: (4t2(t2−1)2)((t2−1)316t6(3t2−5))+α(2tt2+1)(t2−18t5)+βt4=0. t2−14t4(3t2−5)+t2−14αt4(t2+1)+βt4=0. Divide by t4: t2−14(3t2−5)+t2−14α(t2+1)+β=0. Multiply by t2−1: 4(3t2−5)+4α(t2+1)+β(t2−1)=0. 12t2−20+4αt2+4α+βt2−β=0. (12+4α+β)t2+(−20+4α−β)=0. For this to hold for all t, the coefficients must be zero:
- 12+4α+β=0
- −20+4α−β=0 Adding (1) and (2): 8α−8=0⟹α=1. Substituting α=1 into (1): 12+4(1)+β=0⟹16+β=0⟹β=−16. ∣α−β∣=∣1−(−16)∣=∣1+16∣=17.
