Question

If $y = x{e^{ - x}}$, what are the points of inflection of the graph $f(x)$?

Answer 1

Here, we will learn some new concepts like concavity, points of inflection of functions and so on. To find the points of inflection, first we need to find a second derivative of this function. If the first derivative and the second derivative of this functions exist and continuous, the,
The inflection point is $'a'$ for which $f''(a) = 0{\text{ or undefined}}$
We will solve the problem by using some derivative formulas like $\dfrac{d}{{dx}}{e^x} = {e^x}$ and $\dfrac{d}{{dx}}{x^n} = n{x^{n - 1}}$
And also, we will use the product rule which is $\dfrac{d}{{dx}}uv = u\dfrac{d}{{dx}}v + v\dfrac{d}{{dx}}u$ where $u{\text{ and }}v$ are functions in $x$.

Complete step by step answer:
Inflection points are the points at which the graph changes its concavity. Concavity means the concave or convex nature of a graph. It also defines the concave-up or concave-down nature of graphs.
Suppose that there is a function $y = f(x)$.
If the first derivative and the second derivative of this functions exist and continuous, the,
The inflection point is $'a'$ for which $f''(a) = 0{\text{ or undefined}}$
So, in the question, the given function is $y = x{e^{ - x}}$
To find the points of inflection, first we need to find a second derivative of this function.
Let us first find the first derivative.
$y' = \dfrac{d}{{dx}}x{e^{ - x}}$
By applying product rule, (as there are two functions as a single term)
$\Rightarrow y' = x\dfrac{d}{{dx}}{e^{ - x}} + {e^{ - x}}\dfrac{d}{{dx}}x$
$\Rightarrow y' = x( - {e^{ - x}}) + {e^{ - x}}$
So, we get the first derivative as,
$\Rightarrow y' = {e^{ - x}}(1 - x)$
Now, let us find the second derivative.
$y'' = \dfrac{d}{{dx}}{e^{ - x}}(1 - x)$
$\Rightarrow y'' = {e^{ - x}}\dfrac{d}{{dx}}(1 - x) + (1 - x)\dfrac{d}{{dx}}{e^{ - x}}$
Now, on simplification, we get,
$\Rightarrow y'' = - {e^{ - x}} + (1 - x)( - {e^{ - x}})$
$\Rightarrow y'' = {e^{ - x}}(x - 2)$
Now, to get points of inflection, equate the second derivative to zero.
$\Rightarrow y'' = {e^{ - x}}(x - 2) = 0$
So, on solving, we get $x = 2$
So, the point of inflection is $x = 2$.
At this point the graph changes its concavity.

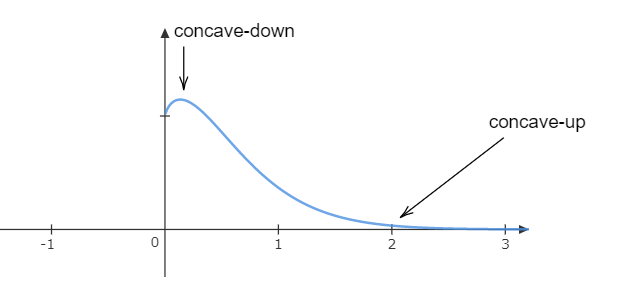
This is the graph for $y = x{e^{ - x}}$.

Note:
In geometry and calculus, the point of inflection is also called inflection point or flex or inflection.
If the function is a decreasing function, then the point of inflection is called A falling point of inflection.
If the function is an increasing function, then the point of inflection is called A rising point of inflection.