Question
Question: If y = f(x) satisfies the differential equation $(1 + x^2)f'(x) = x(1 - f(x))$, $f(0) = \frac{4}{3}$...
If y = f(x) satisfies the differential equation (1+x2)f′(x)=x(1−f(x)), f(0)=34, then find the value of f(8)+98
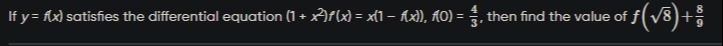
2
Solution
The given differential equation is (1+x2)f′(x)=x(1−f(x)). Rearranging the terms, we get: 1−f(x)f′(x)=1+x2x Integrating both sides: ∫1−fdf=∫1+x2xdx The integral on the left side is −ln∣1−f∣. For the integral on the right side, let u=1+x2, so du=2xdx. The integral becomes ∫u12du=21ln∣u∣=21ln(1+x2). Equating the results: −ln∣1−f∣=21ln(1+x2)+C1 Rearranging and exponentiating: ∣1−f∣=K(1+x2)−1/2 where K=e−C1>0. Thus, the general solution is f(x)=1−A(1+x2)−1/2, where A=±K. Using the initial condition f(0)=34: 34=1−A(1+02)−1/2⟹34=1−A⟹A=−31 So, the particular solution is: f(x)=1−(−31)(1+x2)−1/2=1+31+x21 Now, we find f(8): f(8)=1+31+(8)21=1+31+81=1+391=1+91=910 Finally, we calculate f(8)+98: f(8)+98=910+98=918=2
