Question

If $y = \frac{1}{\sqrt{1-4\sin^2x\cos^2x}}$, then $\frac{dy}{dx} =$

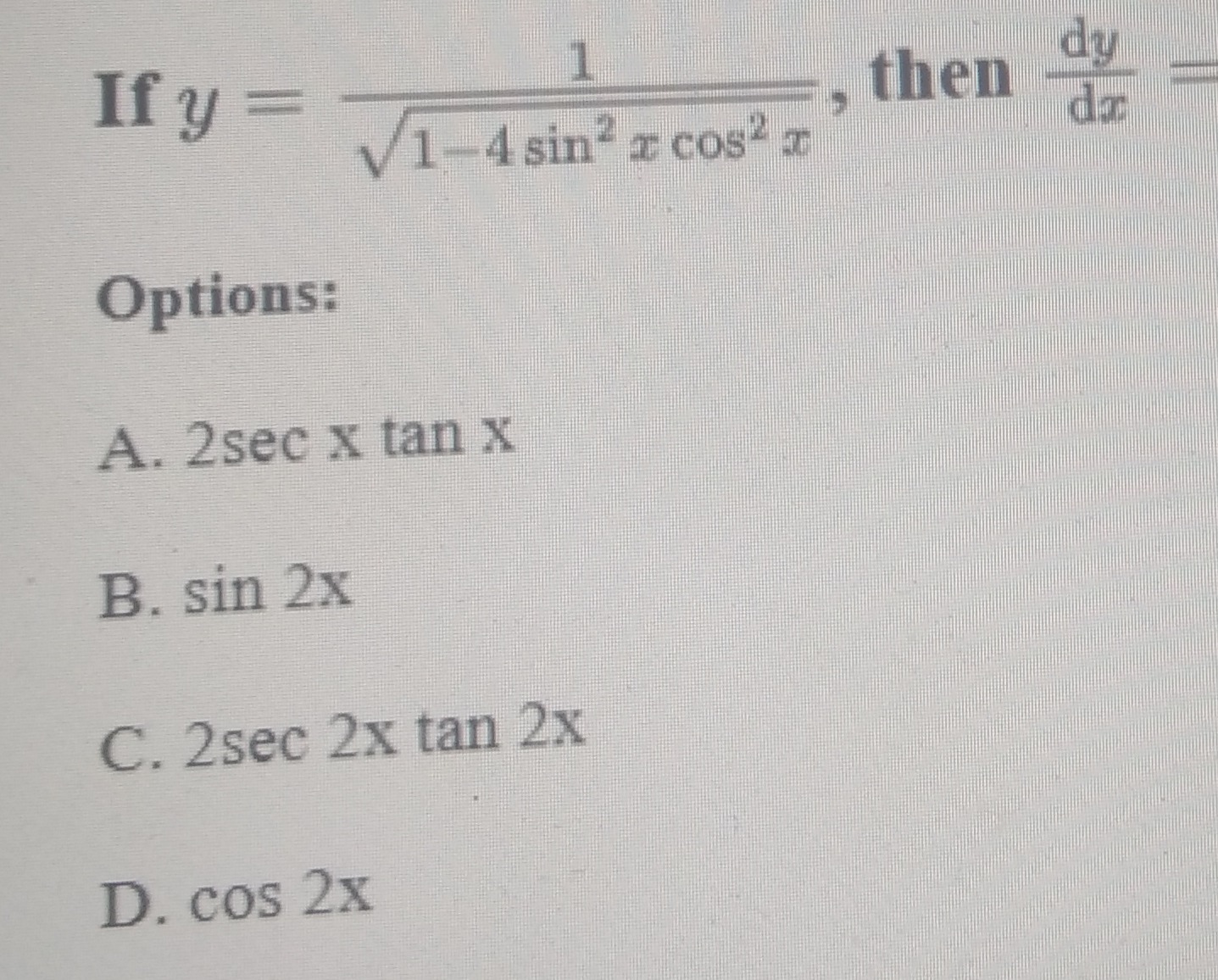
• A. 2sec x tan x
• B. sin 2x
• C. 2sec 2x tan 2x
• D. cos 2x

Answer 1

Answer: (C)

2sec 2x tan 2x

Answer 2

The given function is $y = \frac{1}{\sqrt{1-4\sin^2x\cos^2x}}$.

We can simplify the expression inside the square root using trigonometric identities. We know that $2\sin x\cos x = \sin 2x$. So, $4\sin^2x\cos^2x = (2\sin x\cos x)^2 = (\sin 2x)^2 = \sin^2 2x$. Substitute this into the expression for $y$: $y = \frac{1}{\sqrt{1-\sin^2 2x}}$ Using the identity $1-\sin^2\theta = \cos^2\theta$, we have $1-\sin^2 2x = \cos^2 2x$. So, $y = \frac{1}{\sqrt{\cos^2 2x}}$. The square root of $\cos^2 2x$ is $|\cos 2x|$. Thus, $y = \frac{1}{|\cos 2x|} = |\sec 2x|$.

The question asks for the derivative $\frac{dy}{dx}$. The derivative of $|u|$ is $\text{sgn}(u) \frac{du}{dx}$, where $\text{sgn}(u)$ is the sign function. Here, $u = \sec 2x$. The derivative of $u$ with respect to $x$ is $\frac{du}{dx} = \frac{d}{dx}(\sec 2x)$. Using the chain rule, $\frac{d}{dx}(\sec(ax)) = a\sec(ax)\tan(ax)$. For $a=2$, we have $\frac{d}{dx}(\sec 2x) = 2\sec 2x\tan 2x$. So, $\frac{dy}{dx} = \frac{d}{dx}|\sec 2x| = \text{sgn}(\sec 2x) \cdot (2\sec 2x\tan 2x)$.

The options provided are simple expressions without the sign function or piecewise definition. This suggests that the question might be implicitly considering a domain where $\cos 2x > 0$, which implies $\sec 2x > 0$. In such a domain, $|\sec 2x| = \sec 2x$. Assuming $\cos 2x > 0$, we have $y = \frac{1}{\cos 2x} = \sec 2x$. Now, we differentiate $y = \sec 2x$ with respect to $x$: $\frac{dy}{dx} = \frac{d}{dx}(\sec 2x)$ Using the chain rule, let $u = 2x$. Then $\frac{du}{dx} = 2$. $\frac{dy}{dx} = \frac{d}{du}(\sec u) \cdot \frac{du}{dx} = (\sec u \tan u) \cdot 2 = \sec(2x) \tan(2x) \cdot 2 = 2\sec 2x \tan 2x$.

This result matches option C.