Question
Question: If $x^{(\log_2x)^2-6\log_2x+11}=64$, then x is equal to...
If x(log2x)2−6log2x+11=64, then x is equal to
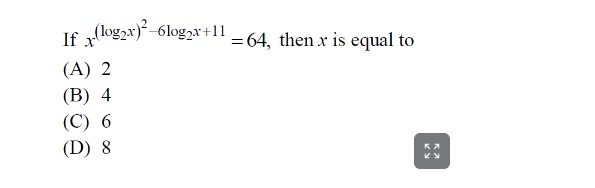
2
4
6
8
2, 4, 8
Solution
To solve the equation x(log2x)2−6log2x+11=64, we follow these steps:
-
Take logarithm on both sides: Since the equation involves log2x, it is convenient to take log2 on both sides of the equation. log2(x(log2x)2−6log2x+11)=log2(64)
-
Apply logarithm properties: Use the property logb(MP)=P⋅logb(M) on the left side and evaluate the right side. The exponent (log2x)2−6log2x+11 comes down as a multiplier. Also, 64=26, so log2(64)=log2(26)=6. ((log2x)2−6log2x+11)⋅log2x=6
-
Substitute a variable: Let y=log2x. This transforms the equation into a polynomial equation in y. (y2−6y+11)⋅y=6 y3−6y2+11y=6
-
Rearrange into a standard polynomial form: y3−6y2+11y−6=0
-
Solve the cubic equation for y: We can find integer roots by testing divisors of the constant term (-6), which are ±1,±2,±3,±6.
- For y=1: 13−6(1)2+11(1)−6=1−6+11−6=0. So, y=1 is a root.
- For y=2: 23−6(2)2+11(2)−6=8−24+22−6=0. So, y=2 is a root.
- For y=3: 33−6(3)2+11(3)−6=27−54+33−6=0. So, y=3 is a root.
Since we found three roots for a cubic equation, these are all the roots. The roots are y=1,y=2,y=3.
-
Substitute back to find x: Now, use y=log2x to find the values of x.
- If y=1: log2x=1⟹x=21⟹x=2
- If y=2: log2x=2⟹x=22⟹x=4
- If y=3: log2x=3⟹x=23⟹x=8
All these values of x (2, 4, 8) are positive, satisfying the domain requirement for logarithms (x>0).
