Question

If $x_i \in \{0, 1, 2\}, y_i \in \{1, 2, 3\}$ then the value of

$\begin{vmatrix} 2x_1y_1 & x_1y_2 + x_2y_1 & x_1y_3 + x_3y_1 \\ x_1y_2 + x_2y_1 & 2x_2y_2 & x_2y_3 + x_3y_2 \\ x_1y_3 + x_3y_1 & x_2y_3 + x_3y_2 & 2x_3y_3 \end{vmatrix}$ is

Answer 1

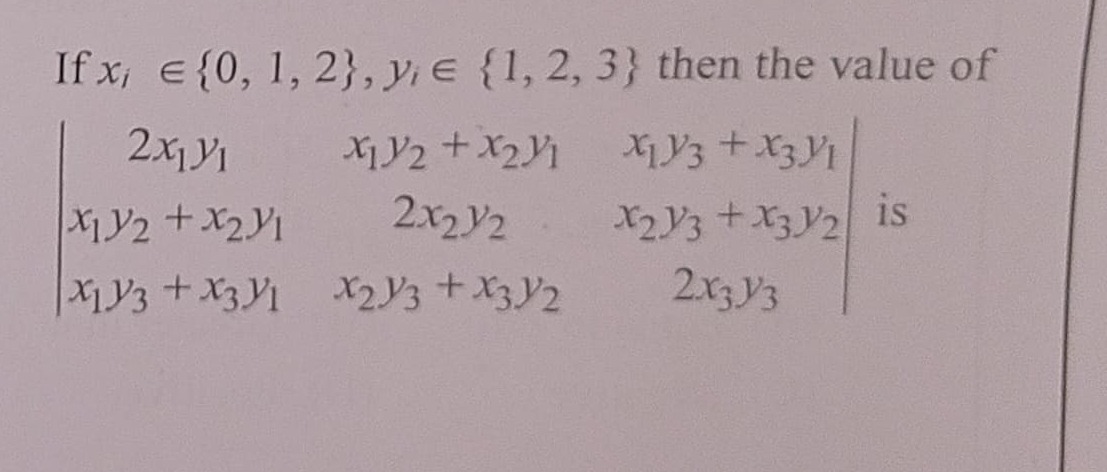
0

Answer 2

Let the given determinant be $D$. The elements of the determinant are $M_{ij}$. Let $\mathbf{x} = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}$ and $\mathbf{y} = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix}$.

Consider the outer product of these two vectors: $A = \mathbf{x} \mathbf{y}^T = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix} \begin{pmatrix} y_1 & y_2 & y_3 \end{pmatrix} = \begin{pmatrix} x_1y_1 & x_1y_2 & x_1y_3 \\ x_2y_1 & x_2y_2 & x_2y_3 \\ x_3y_1 & x_3y_2 & x_3y_3 \end{pmatrix}$.

The transpose of $A$ is: $A^T = (\mathbf{x} \mathbf{y}^T)^T = (\mathbf{y}^T)^T \mathbf{x}^T = \mathbf{y} \mathbf{x}^T = \begin{pmatrix} y_1 \\ y_2 \\ y_3 \end{pmatrix} \begin{pmatrix} x_1 & x_2 & x_3 \end{pmatrix} = \begin{pmatrix} y_1x_1 & y_1x_2 & y_1x_3 \\ y_2x_1 & y_2x_2 & y_2x_3 \\ y_3x_1 & y_3x_2 & y_3x_3 \end{pmatrix}$.

Now, let's form the sum $A + A^T$: $A + A^T = \begin{pmatrix} x_1y_1 & x_1y_2 & x_1y_3 \\ x_2y_1 & x_2y_2 & x_2y_3 \\ x_3y_1 & x_3y_2 & x_3y_3 \end{pmatrix} + \begin{pmatrix} y_1x_1 & y_1x_2 & y_1x_3 \\ y_2x_1 & y_2x_2 & y_2x_3 \\ y_3x_1 & y_3x_2 & y_3x_3 \end{pmatrix}$

$A + A^T = \begin{pmatrix} x_1y_1 + y_1x_1 & x_1y_2 + y_1x_2 & x_1y_3 + y_1x_3 \\ x_2y_1 + y_2x_1 & x_2y_2 + y_2x_2 & x_2y_3 + y_2x_3 \\ x_3y_1 + y_3x_1 & x_3y_2 + y_3x_2 & x_3y_3 + y_3x_3 \end{pmatrix}$

$A + A^T = \begin{pmatrix} 2x_1y_1 & x_1y_2 + x_2y_1 & x_1y_3 + x_3y_1 \\ x_1y_2 + x_2y_1 & 2x_2y_2 & x_2y_3 + x_3y_2 \\ x_1y_3 + x_3y_1 & x_2y_3 + x_3y_2 & 2x_3y_3 \end{pmatrix}$.

This is exactly the matrix given in the problem. So, the problem asks for $\det(A+A^T)$, where $A = \mathbf{x} \mathbf{y}^T$.

The rank of an outer product of two non-zero vectors is 1. Given $x_i \in \{0, 1, 2\}$ and $y_i \in \{1, 2, 3\}$. Since $y_i \in \{1, 2, 3\}$, none of the $y_i$ can be zero, so $\mathbf{y} \neq \mathbf{0}$. If $\mathbf{x} = \mathbf{0}$ (i.e., $x_1=x_2=x_3=0$), then $A = \mathbf{0}$ and $A^T = \mathbf{0}$, so $A+A^T = \mathbf{0}$. The determinant of the zero matrix is 0. If $\mathbf{x} \neq \mathbf{0}$, then $\text{rank}(A) = \text{rank}(\mathbf{x} \mathbf{y}^T) = 1$. Similarly, $\text{rank}(A^T) = \text{rank}(\mathbf{y} \mathbf{x}^T) = 1$.

We know that for any two matrices $P$ and $Q$, $\text{rank}(P+Q) \le \text{rank}(P) + \text{rank}(Q)$. Therefore, $\text{rank}(A+A^T) \le \text{rank}(A) + \text{rank}(A^T) = 1 + 1 = 2$. So, the rank of the matrix $A+A^T$ is at most 2.

The given matrix is a $3 \times 3$ matrix. If the rank of a $n \times n$ matrix is less than $n$, then its determinant is 0. Here, $n=3$ and $\text{rank}(A+A^T) \le 2$, which is less than 3. Thus, the determinant of the given matrix is 0.