Question: If $x^4$ occurs in the $r^{th}$ term in the expansion of \(\left(x^4 + \frac{1}{x^3}\right)^{15}...

Question

If $x^4$ occurs in the $r^{th}$ term in the expansion of $\left(x^4 + \frac{1}{x^3}\right)^{15}$ , then $r=$

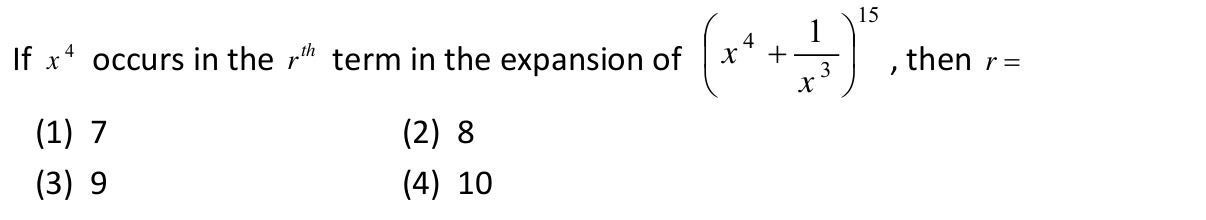
Answer 1

General term in $\bigl(x^4 + x^{-3}\bigr)^{15}$ is

T_{k+1} = \binom{15}{k}(x^4)^{15-k}(x^{-3})^k = \binom{15}{k}\,x^{4(15-k)-3k} = \binom{15}{k}\,x^{60-7k}.

To get $x^4$ , set the exponent equal to 4:

60 - 7k = 4 \quad\Longrightarrow\quad 7k = 56 \quad\Longrightarrow\quad k = 8.

Hence the term is $T_{8+1}=T_9$ . Therefore, $r=9$ .

Question: If \(x^4\) occurs in the \(r^{th}\) term in the expansion of \(\left(x^4 + \frac{1}{x^3}\right)^{15}...