Solveeit Logo
Login

Question

Question: If $x^4 - 2x^3 - 2x^2 + 4x + 3 = 0$ has four real roots $\alpha$, $\beta$, $\gamma$, $\delta$ then $...

If x4−2x3−2x2+4x+3=0x^4 - 2x^3 - 2x^2 + 4x + 3 = 0 has four real roots α\alpha, β\beta, γ\gamma, δ\delta then (1+α2)(1+β2)(1+γ2)(1+δ2)(1+\alpha^2)(1+\beta^2)(1+\gamma^2)(1+\delta^2) is equal to

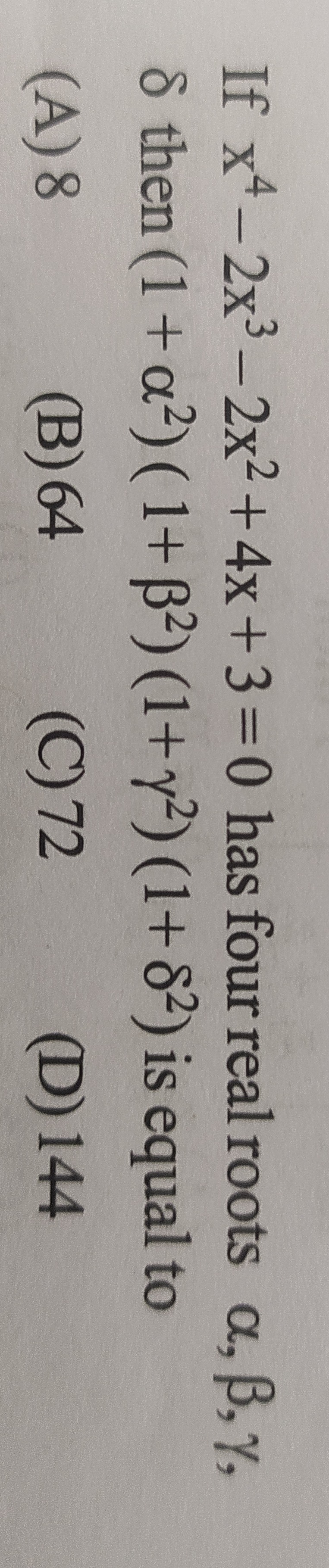
A

8

B

64

C

72

D

144

Answer

72

Explanation

Solution

Given the polynomial

f(x)=x4−2x3−2x2+4x+3=0,f(x) = x^4 - 2x^3 - 2x^2 + 4x + 3 = 0,

with roots α,β,γ,δ\alpha, \beta, \gamma, \delta, we need to calculate

(1+α2)(1+β2)(1+γ2)(1+δ2).(1+\alpha^2)(1+\beta^2)(1+\gamma^2)(1+\delta^2).

Key Step:

Notice that

1+α2=(α−i)(α+i).1 + \alpha^2 = (\alpha - i)(\alpha + i).

Thus,

∏(1+α2)=∏(α−i)(α+i)=f(i)f(−i)(since f(x)=∏(x−α)).\prod (1+\alpha^2)= \prod (\alpha-i)(\alpha+i)= f(i)f(-i) \quad (\text{since } f(x)=\prod (x-\alpha)).

Calculations:

Evaluate f(i)f(i):

f(i)=i4−2i3−2i2+4i+3=1−2(−i)−2(−1)+4i+3(using i2=−1, i3=−i, i4=1)=1+2i+2+4i+3=6+6i.\begin{aligned} f(i) &= i^4 - 2i^3 - 2i^2 + 4i + 3 \\ &= 1 - 2(-i) - 2(-1) + 4i + 3 \quad (\text{using } i^2=-1,\, i^3=-i,\, i^4=1)\\ &= 1 + 2i + 2 + 4i + 3 \\ &= 6 + 6i. \end{aligned}

Evaluate f(−i)f(-i):

f(−i)=(−i)4−2(−i)3−2(−i)2+4(−i)+3=1−2(i)−2(−1)−4i+3(since (−i)2=i2=−1, (−i)3=i, (−i)4=1)=1−2i+2−4i+3=6−6i.\begin{aligned} f(-i) &= (-i)^4 - 2(-i)^3 - 2(-i)^2 + 4(-i) + 3 \\ &= 1 - 2(i) - 2(-1) - 4i + 3 \quad (\text{since } (-i)^2 = i^2 = -1,\, (-i)^3 = i,\, (-i)^4=1)\\ &= 1 - 2i + 2 - 4i + 3 \\ &= 6 - 6i. \end{aligned}

Now,

f(i)f(−i)=(6+6i)(6−6i)=62+62=36+36=72.f(i)f(-i) = (6+6i)(6-6i) = 6^2 + 6^2 = 36 + 36 = 72.