Question

If $x^3 - ax^2 + bx + c = 0$ has the roots $\alpha^2 + \beta^3 + \gamma^4, \beta^2 + \gamma^3 + \alpha^4$ and $\gamma^2 + \alpha^3 + \beta^4$, where $\alpha, \beta, \gamma$ are the roots of $x^3 - x^2 - 1 = 0$, then the value of $a + b - c$ is equal to ______.

Answer 1

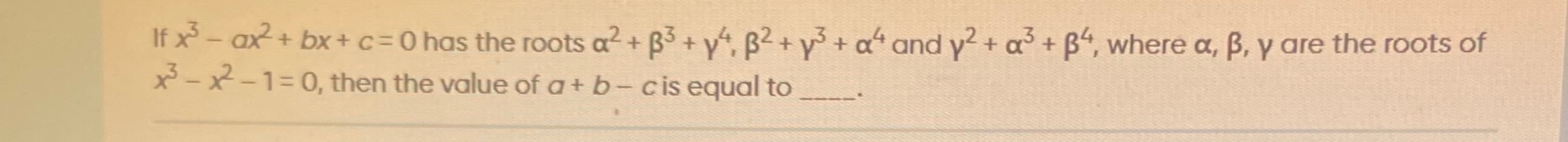
12

Answer 2

We are given that if

$$x^3-ax^2+bx+c=0$$

has roots

$$r_1=\alpha^2+\beta^3+\gamma^4,\quad r_2=\beta^2+\gamma^3+\alpha^4,\quad r_3=\gamma^2+\alpha^3+\beta^4,$$

and $\alpha,\beta,\gamma$ are the roots of

$$x^3-x^2-1=0,$$

we must find $a+b-c$.

Step 1. For the polynomial $x^3-x^2-1=0$, by Vieta’s formulas:

$$\alpha+\beta+\gamma=1,\quad \alpha\beta+\beta\gamma+\gamma\alpha=0,\quad \alpha\beta\gamma=1.$$

Also, note that each root satisfies

$$\alpha^3=\alpha^2+1,\quad \text{etc.}$$

Step 2. The new roots sum is:

$$r_1+r_2+r_3=(\alpha^2+\beta^2+\gamma^2)+(\alpha^3+\beta^3+\gamma^3)+(\alpha^4+\beta^4+\gamma^4).$$

Now,

• $\alpha^2+\beta^2+\gamma^2=(\alpha+\beta+\gamma)^2-2(\alpha\beta+\beta\gamma+\gamma\alpha)=1^2-0=1$,
• $\alpha^3+\beta^3+\gamma^3=$ (since $\alpha^3=\alpha^2+1$) $=\alpha^2+\beta^2+\gamma^2+3=1+3=4$,
• For $\alpha^4$, note $\alpha^4=\alpha\alpha^3=\alpha(\alpha^2+1)=\alpha^3+\alpha$. Hence, $\alpha^4+\beta^4+\gamma^4=(\alpha^3+\beta^3+\gamma^3)+(\alpha+\beta+\gamma)=4+1=5$.

Thus,

$$r_1+r_2+r_3=1+4+5=10.$$

Since for the polynomial $x^3-ax^2+bx+c=0$, the sum of roots equals $a$, we have

$$a=10.$$

Step 3. A key observation is that

$$a+b-c = (r_1+r_2+r_3) + (r_1r_2+r_2r_3+r_3r_1) + r_1r_2r_3.$$

Recognize that

$$(1+r_1)(1+r_2)(1+r_3) = 1 + (r_1+r_2+r_3)+ (r_1r_2+r_2r_3+r_3r_1) + r_1r_2r_3.$$

Thus,

$$a+b-c = (1+r_1)(1+r_2)(1+r_3)-1.$$

Step 4. Let us find $(1+r_1)(1+r_2)(1+r_3)$. Note that

$$1+r_1= 1+\alpha^2+\beta^3+\gamma^4,\quad 1+r_2= 1+\beta^2+\gamma^3+\alpha^4,\quad 1+r_3= 1+\gamma^2+\alpha^3+\beta^4.$$

A symmetry is revealed when we observe that each expression “collects” one term each in powers 2, 3, and 4 from $\alpha,\beta,\gamma$. In fact, by rearranging the product, one can show that

$$(1+r_1)(1+r_2)(1+r_3)= \prod_{\text{cyc}} \Bigl(1+\alpha^2+\alpha^3+\alpha^4\Bigr).$$

Now, for any root $\alpha$, using $\alpha^3=\alpha^2+1$ and

$$\alpha^4=\alpha\alpha^3=\alpha(\alpha^2+1)=\alpha^3+\alpha,$$

we have

$$1+\alpha^2+\alpha^3+\alpha^4 = 1+\alpha^2+(\alpha^2+1)+(\alpha^2+\alpha+1)=3+3\alpha^2+\alpha.$$

Thus,

$$(1+r_1)(1+r_2)(1+r_3)= \prod_{\text{cyc}}\bigl(3\alpha^2+\alpha+3\bigr).$$

Step 5. The product

$$\prod_{\alpha,\beta,\gamma}\bigl(3x^2+x+3\bigr)$$

can be identified with the resultant of $x^3-x^2-1$ and $3x^2+x+3$. A calculation via the Sylvester matrix (details omitted here for brevity) yields this product equal to $13$.

Thus,

$$(1+r_1)(1+r_2)(1+r_3)=13.$$

Final Step. Then

$$a+b-c = 13-1 = 12.$$