Question

If $|x^2-2x+2| - |2x^2-5x+2| = |x^2-3x|$, then the set of value of x is

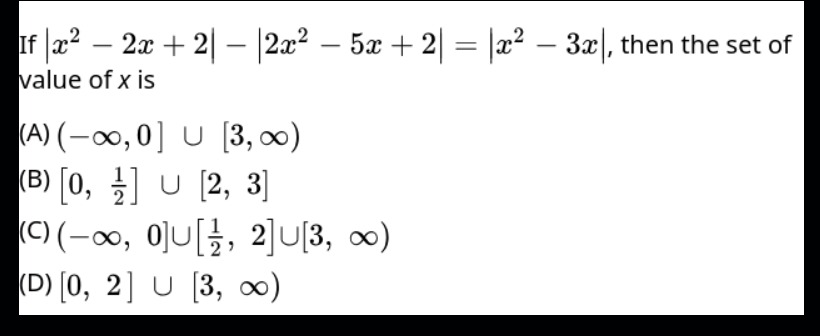
• A. (-\infty,0] \cup [3,\infty)
• B. [0, \frac{1}{2}] \cup [2, 3]
• C. (-\infty, 0]\cup[\frac{1}{2}, 2]\cup[3, \infty)
• D. [0, 2] \cup [3, \infty)

Answer 1

Answer: (B)

[0, \frac{1}{2}] \cup [2, 3]

Answer 2

The given equation is $|x^2-2x+2| - |2x^2-5x+2| = |x^2-3x|$.

Let's define the terms inside the absolute values: Let $A = x^2-2x+2$ Let $B = 2x^2-5x+2$ Let $C = x^2-3x$

The equation can be written as $|A| - |B| = |C|$.

Step 1: Analyze the term $A = x^2-2x+2$. This is a quadratic expression. Its discriminant is $\Delta = (-2)^2 - 4(1)(2) = 4 - 8 = -4$. Since the discriminant is negative ($\Delta < 0$) and the leading coefficient (coefficient of $x^2$) is positive ($1 > 0$), the quadratic $x^2-2x+2$ is always positive for all real values of $x$. Thus, $A > 0$ for all $x \in \mathbb{R}$. Therefore, $|x^2-2x+2| = x^2-2x+2$.

Step 2: Rewrite the equation using the simplified form of $|A|$. The equation becomes $x^2-2x+2 - |2x^2-5x+2| = |x^2-3x|$. This is $A - |B| = |C|$.

Step 3: Find a relationship between $A, B,$ and $C$. Let's compute $A-B$: $A-B = (x^2-2x+2) - (2x^2-5x+2)$ $A-B = x^2-2x+2-2x^2+5x-2$ $A-B = -x^2+3x$ $A-B = -(x^2-3x)$ Notice that $x^2-3x$ is $C$. So, $A-B = -C$. This implies $C = B-A$.

Step 4: Substitute $C = B-A$ into the equation. The equation $A - |B| = |C|$ becomes $A - |B| = |B-A|$. Since $A > 0$, we can write $A = |A|$. So the equation is $|A| - |B| = |B-A|$.

Step 5: Apply the property of absolute values. For any real numbers $X$ and $Y$, the equality $|X| - |Y| = |X-Y|$ holds if and only if $X$ and $Y$ have the same sign (i.e., $XY \ge 0$) AND $|X| \ge |Y|$. In our case, $X=A$ and $Y=B$. Since $A = x^2-2x+2$ is always positive ($A>0$), for $A$ and $B$ to have the same sign, $B$ must also be non-negative ($B \ge 0$). Also, the condition $|A| \ge |B|$ simplifies to $A \ge B$ because both $A$ and $B$ are non-negative.

So, we need to solve the following system of inequalities:

1. $B \ge 0 \implies 2x^2-5x+2 \ge 0$
2. $A \ge B \implies x^2-2x+2 \ge 2x^2-5x+2$

Step 6: Solve inequality 1. $2x^2-5x+2 \ge 0$ To find the roots of $2x^2-5x+2=0$, we can factor it: $(2x-1)(x-2)=0$. The roots are $x = \frac{1}{2}$ and $x = 2$. Since the parabola $y=2x^2-5x+2$ opens upwards (coefficient of $x^2$ is $2>0$), the expression is non-negative when $x$ is outside or on the roots. So, $x \in (-\infty, \frac{1}{2}] \cup [2, \infty)$.

Step 7: Solve inequality 2. $x^2-2x+2 \ge 2x^2-5x+2$ Rearrange the terms to one side: $0 \ge 2x^2-x^2-5x+2x+2-2$ $0 \ge x^2-3x$ This can be written as $x^2-3x \le 0$. Factor the expression: $x(x-3) \le 0$. The roots of $x(x-3)=0$ are $x=0$ and $x=3$. Since the parabola $y=x^2-3x$ opens upwards (coefficient of $x^2$ is $1>0$), the expression is non-positive when $x$ is between or on the roots. So, $x \in [0, 3]$.

Step 8: Find the intersection of the solution sets from inequality 1 and inequality 2. We need $x \in \left( (-\infty, \frac{1}{2}] \cup [2, \infty) \right) \cap [0, 3]$. Let's find the intersection of each part:

• $(-\infty, \frac{1}{2}] \cap [0, 3] = [0, \frac{1}{2}]$
• $[2, \infty) \cap [0, 3] = [2, 3]$

Combining these two intervals, the solution set is $[0, \frac{1}{2}] \cup [2, 3]$.

The final answer is $[0, \frac{1}{2}] \cup [2, 3]$.