Question
Question: If x, y, z ∈ R & $\Delta = \begin{vmatrix} x & x+y & x+y+z \\ 2x & 5x+2y & 7x+5y+2z \\ 3x & 7x+3y & ...
If x, y, z ∈ R & Δ=x2x3xx+y5x+2y7x+3yx+y+z7x+5y+2z9x+7y+3z=−16 then value of x is
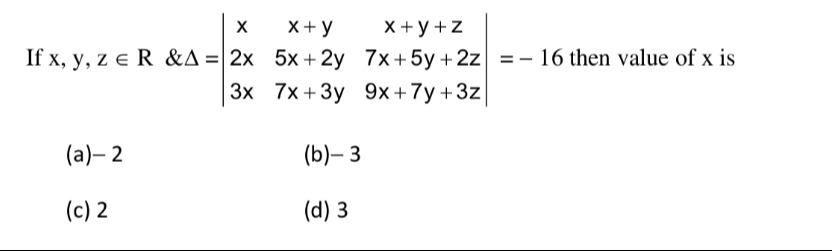
-2
-3
2
3
2
Solution
The given determinant is Δ=x2x3xx+y5x+2y7x+3yx+y+z7x+5y+2z9x+7y+3z. We are given that Δ=−16.
We can simplify the determinant using column operations. Apply the operation C2←C2−C1:
Δ=x2x3x(x+y)−x(5x+2y)−2x(7x+3y)−3xx+y+z7x+5y+2z9x+7y+3z=x2x3xy3x+2y4x+3yx+y+z7x+5y+2z9x+7y+3z
Apply the operation C3←C3−C2:
Δ=x2x3xy3x+2y4x+3y(x+y+z)−(x+y)(7x+5y+2z)−(5x+2y)(9x+7y+3z)−(7x+3y)=x2x3xy3x+2y4x+3yz2x+3y+2z2x+4y+3z
Now, apply row operations to simplify the determinant further. Apply the operation R2←R2−2R1: The new R2 is (2x−2x,(3x+2y)−2y,(2x+3y+2z)−2z)=(0,3x,2x+3y).
Apply the operation R3←R3−3R1: The new R3 is (3x−3x,(4x+3y)−3y,(2x+4y+3z)−3z)=(0,4x,2x+4y).
The determinant becomes: Δ=x00y3x4xz2x+3y2x+4y
Expand the determinant along the first column:
Δ=x⋅3x4x2x+3y2x+4y−0⋅y4xz2x+4y+0⋅y3xz2x+3y
Δ=x[(3x)(2x+4y)−(4x)(2x+3y)]
Δ=x[(6x2+12xy)−(8x2+12xy)]
Δ=x[6x2+12xy−8x2−12xy]
Δ=x[−2x2]
Δ=−2x3
We are given that Δ=−16. So, −2x3=−16. Divide both sides by -2: x3=−2−16
x3=8
Since x∈R, the only real solution is the cube root of 8. x=38
x=2
The value of x is 2.
