Question
Question: If x, y are integral solutions of $2x^2 - 3xy - 2y^2 = 7$, then the value of |x + y| is...
If x, y are integral solutions of 2x2−3xy−2y2=7, then the value of |x + y| is
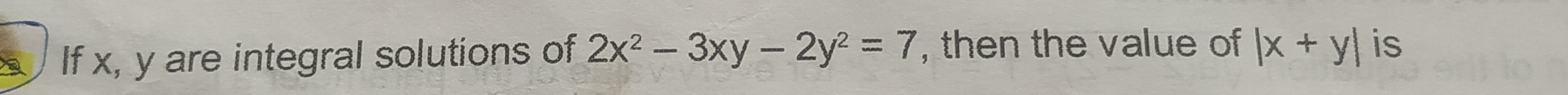
5
6
3
4
4
Solution
The given equation is 2x2−3xy−2y2=7. We need to find integral solutions (x,y). The left side of the equation can be factored. We can treat it as a quadratic in x: 2x2−(3y)x−2y2. We look for factors of the form (ax+by)(cx+dy). The product of the x2 coefficients must be 2, so ac=2. Possible pairs for (a,c) are (1,2) or (2,1) or (−1,−2) or (−2,−1). The product of the y2 coefficients must be -2, so bd=−2. Possible pairs for (b,d) are (1,−2),(−1,2),(2,−1),(−2,1). The coefficient of xy is ad+bc=−3.
Let's try the form (x+by)(2x+dy). ad+2b=−3. If (b,d)=(1,−2), then 1(−2)+2(1)=−2+2=0=−3. If (b,d)=(−1,2), then 1(2)+2(−1)=2−2=0=−3. If (b,d)=(2,−1), then 1(−1)+2(2)=−1+4=3=−3. If (b,d)=(−2,1), then 1(1)+2(−2)=1−4=−3. This works. So the factors are (x−2y)(2x+y).
Let's verify the factorization: (x−2y)(2x+y)=x(2x+y)−2y(2x+y)=2x2+xy−4xy−2y2=2x2−3xy−2y2. The factorization is correct. So the equation is (x−2y)(2x+y)=7. Since x and y are integers, the factors (x−2y) and (2x+y) must be integer factors of 7. The integer factors of 7 are 1,−1,7,−7. We have four possible cases for the values of the factors:
Case 1: x−2y=1 and 2x+y=7. Multiply the second equation by 2: 4x+2y=14. Add the first equation to this: (x−2y)+(4x+2y)=1+14⟹5x=15⟹x=3. Substitute x=3 into 2x+y=7: 2(3)+y=7⟹6+y=7⟹y=1. So (x,y)=(3,1) is an integral solution. For this solution, ∣x+y∣=∣3+1∣=∣4∣=4.
Case 2: x−2y=7 and 2x+y=1. Multiply the second equation by 2: 4x+2y=2. Add the first equation to this: (x−2y)+(4x+2y)=7+2⟹5x=9⟹x=9/5. This is not an integer, so there is no integral solution in this case.
Case 3: x−2y=−1 and 2x+y=−7. Multiply the second equation by 2: 4x+2y=−14. Add the first equation to this: (x−2y)+(4x+2y)=−1+(−14)⟹5x=−15⟹x=−3. Substitute x=−3 into 2x+y=−7: 2(−3)+y=−7⟹−6+y=−7⟹y=−1. So (x,y)=(−3,−1) is an integral solution. For this solution, ∣x+y∣=∣−3+(−1)∣=∣−4∣=4.
Case 4: x−2y=−7 and 2x+y=−1. Multiply the second equation by 2: 4x+2y=−2. Add the first equation to this: (x−2y)+(4x+2y)=−7+(−2)⟹5x=−9⟹x=−9/5. This is not an integer, so there is no integral solution in this case.
The integral solutions are (3,1) and (−3,−1). For both solutions, the value of ∣x+y∣ is 4.
