Question

If x + y = 3 is the equation of the chord AB of the circle ${{x}^{2}}+{{y}^{2}}-2x+4y-8=0$, find the equation of the circle having AB as diameter.

Answer 1

Hint : Find the intersection of chord and circle to get the relation between the coordinates of a given chord. Find the center as the midpoint of the chord and length gives the diameter. You do not need to calculate the exact points of the intersection just use the relation between them.

Complete step by step solution :
Here, we are given a chord x + y = 3 to a circle ${{x}^{2}}+{{y}^{2}}-2x+4y-8=0$ as shown in the diagram.

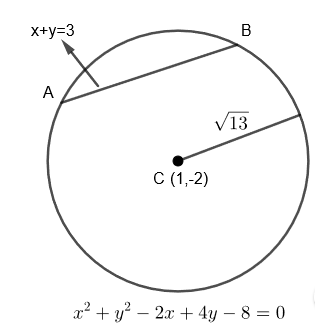
To find center and radius, let us compare the given equation with the standard equation:
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
Where (-g, -f) is the center and radius is $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$.
Hence, the center of a given circle is (1, -2).
And radius $=\sqrt{{{1}^{2}}+{{\left( -2 \right)}^{2}}-\left( -8 \right)}$
$=\sqrt{1+4+8}$
Radius $=\sqrt{13}$
Here, we have the given chord x + y = 3 which we need to take as diameter and find that circle. So, we need to find coordinates of A and B to get the radius and center.
Let the point A be $\left( {{x}_{1}},{{y}_{1}} \right)$and point B be $\left( {{x}_{2}},{{y}_{2}} \right)$.

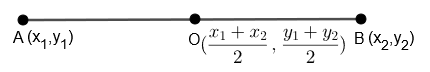
Hence, the center can be written as the midpoint of $AB=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{y_{1}}+{{y}_{2}}}{2} \right)$
Now, let us find out the intersection of the given chord and circle:
Equation of chord given is: x + y = 3
Or $y=3-x.....\left( i \right)$
Now, let us put the value of equation (i) in equation of the circle given as ${{x}^{2}}+{{y}^{2}}-2x+4y-8=0$to get intersection points.
${{x}^{2}}+{{\left( 3-x \right)}^{2}}-2x+4\left( 3-x \right)-8=0$
${{x}^{2}}+9+{{x}^{2}}-6x-2x+12-4x-8=0$
$2{{x}^{2}}-12x+13=0.....\left( ii \right)$
As we can see that equation (ii) is quadratic in ‘x’ and on solving it, will give two values of ‘x’ which is none other than ${{x}_{1}}$ and ${{x}_{2}}$ i.e. intersecting points.
Hence, ${{x}_{1}},{{x}_{2}}$ are roots of the given quadratic equation (ii).
So, if $\alpha$and $\beta$are two roots of the quadratic equation: $A{{x}^{2}}+Bx+C=0$, then
$\alpha +\beta =\dfrac{-B}{A}$
And $\alpha \beta =\dfrac{C}{A}$
Hence from the quadratic equation (ii), we have
$2{{x}^{2}}-12x+13=0$
${{x}_{1}}+{{x}_{2}}=\dfrac{12}{2}=6.....\left( iii \right)$
${{x}_{1}}{{x}_{2}}=\dfrac{13}{2}....\left( iv \right)$
Similarly, on substituting x = 3 – y from the equation of chord to the equation of the circle, we can get quadratic in form of ‘y’ in the following way:
${{x}^{2}}+{{y}^{2}}-2x+4y-8=0$
${{\left( 3-y \right)}^{2}}+{{y}^{2}}-2\left( 3-y \right)+4y-8=0$
$9+{{y}^{2}}-6y+{{y}^{2}}-6+2y+4y-8=0$
$2{{y}^{2}}-5=0$
${{y}^{2}}=\dfrac{5}{2}$
$y=\pm \sqrt{\dfrac{5}{2}}$
Hence, these points are ‘y’ coordinates of intersection points of chord and circle.
Therefore, ${{y}_{1}}+{{y}_{2}}=\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{5}{2}}=0$
${{y}_{1}}+{{y}_{2}}=0.....\left( v \right)$
${{y}_{1}}{{y}_{2}}=\dfrac{-5}{2}....\left( vi \right)$
Now, let us calculate the equation of circle as
Center $=\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$
$=\left( \dfrac{6}{2},0 \right)=\left( 3,0 \right)$
Diameter length $=\sqrt{{{\left( {{x}_{1}}-{{x}_{2}} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{2}} \right)}^{2}}}$
Here, we can use the relationship
${{\left( a-b \right)}^{2}}={{\left( a+b \right)}^{2}}-4ab$
So, we can rewrite the length of diameter as
$\sqrt{{{\left( {{x}_{1}}+{{x}_{2}} \right)}^{2}}-4{{x}_{1}}{{x}_{2}}+{{\left( {{y}_{1}}+{{y}_{2}} \right)}^{2}}-4{{y}_{1}}{{y}_{2}}}$
Putting the required values from equations (iii), (iv), (v) and (vi), we get
$\text{Diameter}=\sqrt{{{\left( 6 \right)}^{2}}-4\times \dfrac{13}{2}+0-4\times \left( \dfrac{-5}{2} \right)}$
$=\sqrt{36-26+10}$
$=\sqrt{20}=2\sqrt{5}$
Hence, the radius $=\dfrac{2\sqrt{5}}{2}=\sqrt{5}$
We know the equation of the circle in radius and center form can be written as ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$
where $\left( {{x}_{1}},{{y}_{1}} \right)$ is the center and ‘r’ is the radius.
$\left( {{x}_{1}}{{y}_{1}} \right)=\left( {{31}^{o}} \right)$
And radius $=\sqrt{5}$
We can write the equation of the circle as
${{\left( x-3 \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \sqrt{5} \right)}^{2}}$
${{x}^{2}}+9-6x+{{y}^{2}}=5$
${{x}^{2}}+{{y}^{2}}-6x+4=0$

Note : We can use the diameter form of the equation of a circle to get the equation after calculating $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$.
As $\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0$
${{x}^{2}}-x\left( {{x}_{1}}+{{x}_{2}} \right)+{{x}_{1}}{{x}_{2}}+{{y}^{2}}-y\left( {{y}_{1}}+{{y}_{2}} \right)+{{y}_{1}}{{y}_{2}}=0$
${{x}^{2}}-6x+\dfrac{13}{2}+{{y}^{2}}-0-\dfrac{5}{2}=0$
${{x}^{2}}+{{y}^{2}}-6x+4=0$
We can also solve the quadratic (ii) to get the values of ${{x}_{1}}$ and ${{x}_{2}}$ and directly calculate the equation of the circle. But here, we can see that we do not need to calculate exact values of $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$. We only need to know (${x_{1}}+{{x}_{2}},{{x}_{1}}{{x}_{2}},{{y}_{1}}+{{y}_{2}},{{y}_{1}}{{y}_{2}}$) values which can be obtained from the quadratic directly.
We have one more method to solve this question. We can draw a perpendicular from center to chord which will bisect it.

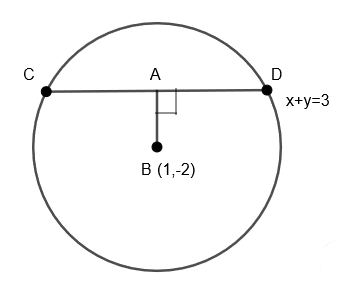
We can write the equation of $AB$ which has slope ‘1’ as ‘x + y = 3’ and slope (-1), and it will pass through (1, -2). So, we can write the equation of it as ‘y + 2 = 1(x – 1)’.
$y+2=x-1$
$x-y=3$
We can find a point A(3, 0) by solving ‘x – y = 3’ and ‘x + y = 3’. Now, AC can be calculated by $\sqrt{B{{C}^{2}}-A{{B}^{2}}}$ where BC is the radius of the given circle and AB is perpendicular from the center to the chord which can be calculated as the following way.
Perpendicular length of any point$\left( {{x}_{1}},{{y}_{1}} \right)$ from the line $Ax+By+C=0$ is:
$\left| \dfrac{A{{x}_{1}}+B{{y}_{1}}+C}{\sqrt{{{A}^{2}}+{{B}^{2}}}} \right|$
Hence, AC will be the radius and A will be the center. So, we can find the equation of a circle from here as well.