Question

If x - y + 1 = 0 meets the circle ${x^2} + {y^2} + y - 1 = 0$ at A,B then the equation of the circle with AB as diameter
A) $2\left( {{x^2} + {y^2}} \right) + 3x - y + 1 = 0$
B) $2\left( {{x^2} + {y^2}} \right) + 3x - y + 2 = 0$
C) $2\left( {{x^2} + {y^2}} \right) + 3x - y + 3 = 0$
D) ${x^2} + {y^2} + 3x - y + 1 = 0$

Answer 1

Hint: First of all draw the required figure then find the radius of the given circle also find the foot of perpendicular from the center of the given circle then you can easily see that the midpoint of AB lies on the radius of the circle and we can easily get the by pythagoras theorem.
Complete Step by Step Solution:
Let us try to draw the figure first

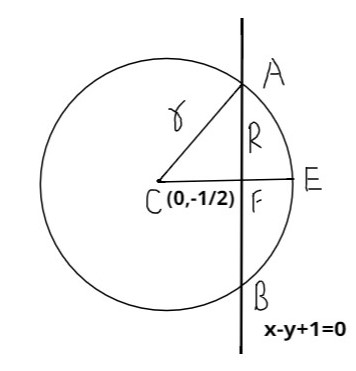
It is given that the equation of the circle is ${x^2} + {y^2} + y - 1 = 0$
It can be written as

{x^2} + {\left( {y - \dfrac{1}{2}} \right)^2} = 1 + \dfrac{1}{4}\\\ \Rightarrow {x^2} + {\left( {y - \dfrac{1}{2}} \right)^2} = \dfrac{5}{4} \end{array}$$ Now if we compare this with the general equation of circles we will get it as $${(x - h)^2} + {\left( {y - k} \right)^2} = {r^2}$$ where (h,k) is the center of the circle and r is the radius of the circle $$\therefore r = \sqrt {\dfrac{5}{4}} = \dfrac{{\sqrt 5 }}{2}$$ also the centre of the circle is $$\left( {0, - \dfrac{1}{2}} \right)$$ Now the foot of perpendicular from $$C\left( {0, - \dfrac{1}{2}} \right)$$ on $$x - y + 1 = 0$$ given midpoint on diameter AB i.e., point E $$\therefore \dfrac{{x - 0}}{1} = \dfrac{{y - \dfrac{1}{2}}}{{ - 1}} = - 1\dfrac{{\dfrac{3}{2}}}{{{1^2} + {1^2}}} = \dfrac{{ - 3}}{4}$$ From here we can say that $$\begin{array}{l} x = \dfrac{{ - 3}}{4}\& y = \dfrac{1}{4}\\\ \therefore E\left( {\dfrac{{ - 3}}{4},\dfrac{1}{4}} \right) \end{array}$$ So radius of circle having AB as diameter is $$R = \sqrt {{r^2} - {{(CF)}^2}} = \sqrt {\dfrac{5}{4} - \dfrac{9}{8}} = \sqrt {\dfrac{1}{8}} = \dfrac{1}{{2\sqrt 2 }}$$ Therefore equation of circle having AB as diameter, $$\begin{array}{l} \Rightarrow {\left( {x + \dfrac{3}{4}} \right)^2} + {\left( {y - \dfrac{1}{2}} \right)^2} = {\left( {\dfrac{1}{{2\sqrt 2 }}} \right)^2}\\\ \Rightarrow 2\left( {{x^2} + {y^2}} \right) + 3x - y + 2 = 0 \end{array}$$ So clearly Option (B) is the correct option. Note: The figure was the key to solving this question. One must know what he is trying to find and extract it from the given data. Here all we needed was the radius of the circle we are told to find once we got that it was only a matter of time to put it and get the final equation.