Solveeit Logo
Login

Question

Question: If $x = \sqrt{3 + 2\sqrt{2}}$, then value of $x^2 + \frac{1}{x^2}$ is equal to...

If x=3+22x = \sqrt{3 + 2\sqrt{2}}, then value of x2+1x2x^2 + \frac{1}{x^2} is equal to

A

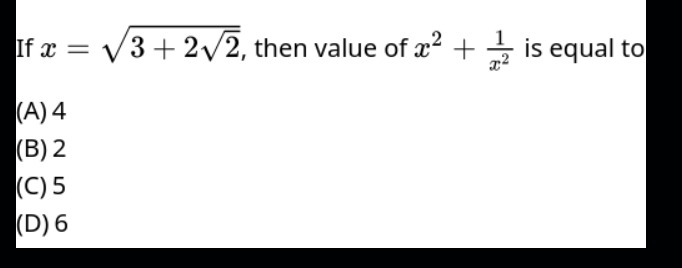
4

B

2

C

5

D

6

Answer

6

Explanation

Solution

To find the value of x2+1x2x^2 + \frac{1}{x^2}, we first need to simplify the expression for xx.

Given: x=3+22x = \sqrt{3 + 2\sqrt{2}}

We can simplify the term inside the square root by recognizing it as a perfect square. Consider the identity (a+b)2=a2+b2+2ab(a+b)^2 = a^2 + b^2 + 2ab. We want to express 3+223 + 2\sqrt{2} in the form a2+b2+2aba^2 + b^2 + 2ab. Let 2ab=222ab = 2\sqrt{2}, which implies ab=2ab = \sqrt{2}. Also, we need a2+b2=3a^2 + b^2 = 3. If we choose a=2a = \sqrt{2} and b=1b = 1, then ab=2⋅1=2ab = \sqrt{2} \cdot 1 = \sqrt{2} (satisfies the first condition). And a2+b2=(2)2+12=2+1=3a^2 + b^2 = (\sqrt{2})^2 + 1^2 = 2 + 1 = 3 (satisfies the second condition). So, 3+22=(2+1)23 + 2\sqrt{2} = (\sqrt{2} + 1)^2.

Now substitute this back into the expression for xx: x=(2+1)2x = \sqrt{(\sqrt{2} + 1)^2} x=2+1x = \sqrt{2} + 1

Next, we need to find x2x^2 and 1x2\frac{1}{x^2}.

  1. Calculate x2x^2: x2=(2+1)2x^2 = (\sqrt{2} + 1)^2 x2=(2)2+12+2⋅2⋅1x^2 = (\sqrt{2})^2 + 1^2 + 2 \cdot \sqrt{2} \cdot 1 x2=2+1+22x^2 = 2 + 1 + 2\sqrt{2} x2=3+22x^2 = 3 + 2\sqrt{2}

  2. Calculate 1x2\frac{1}{x^2}: First, let's find 1x\frac{1}{x}: 1x=12+1\frac{1}{x} = \frac{1}{\sqrt{2} + 1} To rationalize the denominator, multiply the numerator and denominator by the conjugate of the denominator, which is 2−1\sqrt{2} - 1: 1x=12+1×2−12−1\frac{1}{x} = \frac{1}{\sqrt{2} + 1} \times \frac{\sqrt{2} - 1}{\sqrt{2} - 1} 1x=2−1(2)2−12\frac{1}{x} = \frac{\sqrt{2} - 1}{(\sqrt{2})^2 - 1^2} 1x=2−12−1\frac{1}{x} = \frac{\sqrt{2} - 1}{2 - 1} 1x=2−11\frac{1}{x} = \frac{\sqrt{2} - 1}{1} 1x=2−1\frac{1}{x} = \sqrt{2} - 1

    Now, calculate 1x2\frac{1}{x^2}: 1x2=(1x)2=(2−1)2\frac{1}{x^2} = \left(\frac{1}{x}\right)^2 = (\sqrt{2} - 1)^2 1x2=(2)2+12−2⋅2⋅1\frac{1}{x^2} = (\sqrt{2})^2 + 1^2 - 2 \cdot \sqrt{2} \cdot 1 1x2=2+1−22\frac{1}{x^2} = 2 + 1 - 2\sqrt{2} 1x2=3−22\frac{1}{x^2} = 3 - 2\sqrt{2}

  3. Calculate x2+1x2x^2 + \frac{1}{x^2}: x2+1x2=(3+22)+(3−22)x^2 + \frac{1}{x^2} = (3 + 2\sqrt{2}) + (3 - 2\sqrt{2}) x2+1x2=3+22+3−22x^2 + \frac{1}{x^2} = 3 + 2\sqrt{2} + 3 - 2\sqrt{2} x2+1x2=3+3+(22−22)x^2 + \frac{1}{x^2} = 3 + 3 + (2\sqrt{2} - 2\sqrt{2}) x2+1x2=6+0x^2 + \frac{1}{x^2} = 6 + 0 x2+1x2=6x^2 + \frac{1}{x^2} = 6