Solveeit Logo
Login

Question

Question: If \( x={{\sin }^{-1}}(\sin 10) \) and \( y={{\cos }^{-1}}(\cos 10) \) , then y – x is equals to...

If x=sin⁡−1(sin⁡10)x={{\sin }^{-1}}(\sin 10) and y=cos⁡−1(cos⁡10)y={{\cos }^{-1}}(\cos 10) , then y – x is equals to

Explanation

Solution

Hint : To solve this question we will take the help of graph of functions y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) and y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) . What we will do is we will check on which line the value 10 on graph y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) and y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) as graphs of functions y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) and y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) are continuous.
Then, finally we will evaluate the value of y and x and hence find y – x .

Complete step-by-step answer :
Before we solve the question to get value of y – x ,
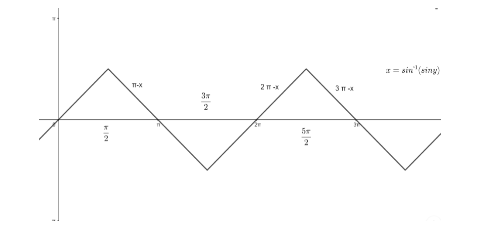
Let us see the properties and graph of function y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) .
sin⁡−1(sinx⁡)=−π−x;−3π2≤x≤−π2{{\sin }^{-1}}(\operatorname{sinx})=-\pi -x;\dfrac{-3\pi }{2}\le x\le \dfrac{-\pi }{2} ,
=x;−π2≤x≤π2=x;\dfrac{-\pi }{2}\le x\le \dfrac{\pi }{2} ,
=π;π2≤x≤3π2=\pi ;\dfrac{\pi }{2}\le x\le \dfrac{3\pi }{2} .
And, graph of y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) is given as ,

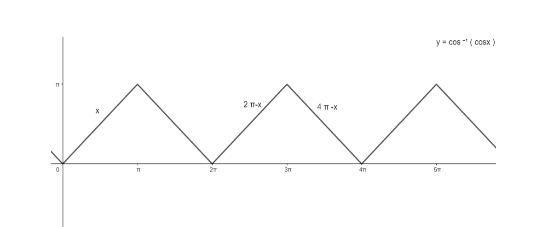
Let us see the properties and graph of the function y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) .
cos⁡−1(cosx)=−x;−π≤x≤0{{\cos }^{-1}}(cosx)=-x;-\pi \le x\le 0
=x;0≤x≤π=x;0\le x\le \pi
=2π−x;π≤x≤2π=2\pi -x;\pi \le x\le 2\pi
And, graph of y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) is given as ,

Now, let us solve for x=sin⁡−1(sin⁡10)x={{\sin }^{-1}}(\sin 10) first,
As we see that, 5π2≤10≤7π2\dfrac{5\pi }{2}\le 10\le \dfrac{7\pi }{2}
So, we can say that 10 lies on line 3π−x3\pi -x , so 10 will satisfy the equation y=3π−xy=3\pi -x
Putting x = 10 in y=3π−xy=3\pi -x , we get
y=3π−10y=3\pi -10 .
Or, 3π−10=sin⁡−1(sin⁡10)3\pi -10={{\sin }^{-1}}(\sin 10) …… ( i )
Now, let us solve for y=cos⁡−1(cos10)y={{\cos }^{-1}}(cos10) ,
As we see that, 3π≤10≤4π3\pi \le 10\le 4\pi ,
So, we can say that 10 lies on line 4π−x4\pi -x , so 10 will satisfy the equation y=4π−xy=4\pi -x
Putting x = 10 in y=4π−xy=4\pi -x , we get
y=4π−10y=4\pi -10 .
Or, 4π−10=cos⁡−1(cos10)4\pi -10={{\cos }^{-1}}(cos10) …..( ii )
Now, we have to find the value of, y – x that is cos⁡−1(cos10)−sin⁡−1(sin⁡10){{\cos }^{-1}}(cos10)-{{\sin }^{-1}}(\sin 10) ,which is equals to
y−x=(4π−10)−(3π−10)y-x=(4\pi -10)-(3\pi -10) .

Note : Graph of y=sin⁡−1(sinx⁡)y={{\sin }^{-1}}(\operatorname{sinx}) and y=cos⁡−1(cosx)y={{\cos }^{-1}}(cosx) are very important function and graphs should be remembered while solving questions based on inverse trigonometric functions. The value of input should be checked on which line of the function does it lie carefully as it may change the output of the function.