Solveeit Logo
Login

Question

Question: If \(x={{\sin }^{-1}}\left( \sin 10 \right)\) and \(y={{\cos }^{-1}}\left( \cos 10 \right)\) then \(...

If x=sin⁡−1(sin⁡10)x={{\sin }^{-1}}\left( \sin 10 \right) and y=cos⁡−1(cos⁡10)y={{\cos }^{-1}}\left( \cos 10 \right) then y−x=y-x=?
(a) π\pi
(b) 0
(c) π−20\pi -20
(d) 2π2\pi

Explanation

Solution

Here, first let us draw the graph and mention which trigonometric functions are positive in which quadrant. Use the basic principles of sine and cosine functions and the angle in which they are positive. Convert the given angle into the obtained angle and then use basic operation of subtraction to find the result.

Complete step-by-step answer:
Here, we have been given x=sin⁡−1(sin⁡10)x={{\sin }^{-1}}\left( \sin 10 \right) and y=cos⁡−1(cos⁡10)y={{\cos }^{-1}}\left( \cos 10 \right). Let us first draw a graph and the significance of trigonometric functions in the graph.

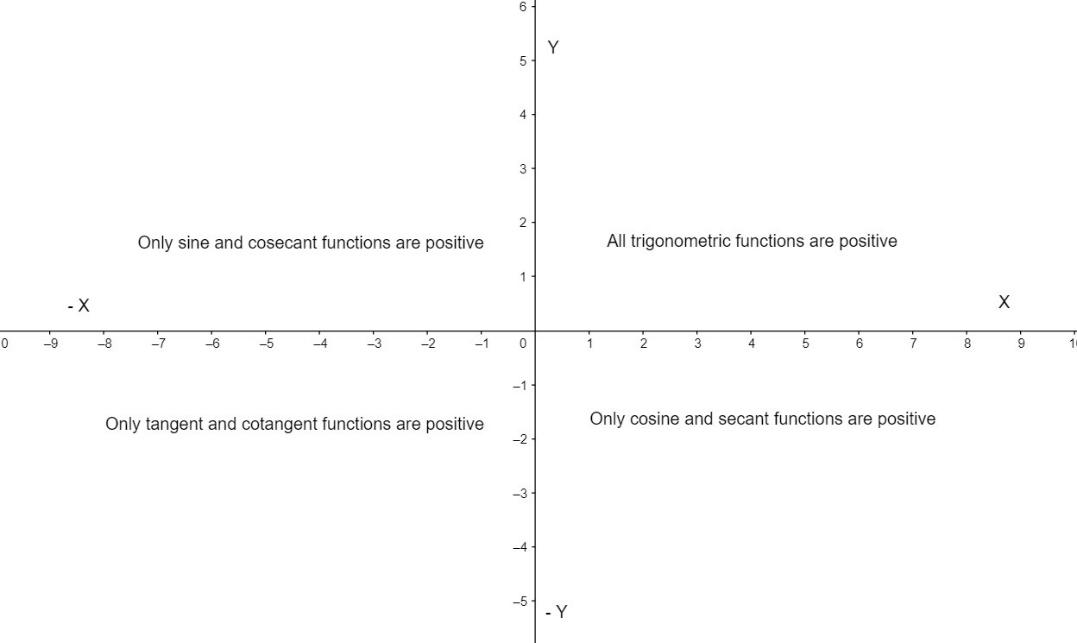
From the given values, we can see that in sin (10) and cos (10) has no value because sin⁡−1x{{\sin }^{-1}}x ∈(−π2, π2)\in \left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right), hence we shall find the value of xx. Also, π\pi = 3.141.
Now, we know that the sine function is positive in 1st and 2nd quadrant, and hence, sine function is positive for π−θ\pi -\theta , 2π+θ2\pi +\theta and 3π−θ3\pi -\theta . We know, (−π2, π2)=(−1.57, 1.57)\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)=\left( -1.57,\,1.57 \right)
For, π−10\pi -10:
π−10\pi -10 = 3.141 – 10 = – 6.85, this does not lie within (−π2, π2)\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)
For, 2π+102\pi +10:
2π+102\pi +10 = 2 (3.141) + 10 = 16.28, this does not lie within (−π2, π2)\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)
For, 3π−103\pi -10:
3π−103\pi -10 = 3 (3.141) – 10 = – 0.57, this lies within (−π2, π2)\left( -\dfrac{\pi }{2},\,\dfrac{\pi }{2} \right)
Therefore, we can write sin (10) as sin (3π−103\pi -10).
Now, x=sin⁡−1[sin⁡(3π−10)]x={{\sin }^{-1}}\left[ \sin \left( 3\pi -10 \right) \right]
We get, x=3π−10x=3\pi -10…………. (1)
Now, let us find the value of yy,
For cosine functions, we can see that cosine is only positive in the 4th quadrant and 1st quadrant. Since cosine is an even function we can use 0, 2π2\pi , 4π4\pi . We know that, cos⁡−1{{\cos }^{-1}} ∈(−π,  π)\in \left( -\pi ,\,\,\pi \right). We will get cosine as positive in 2π−θ2\pi -\theta , 2π+θ2\pi +\theta , 4π−θ4\pi -\theta . (−π,  π)=(−3.141,  3.141)\left( -\pi ,\,\,\pi \right)=\left( -3.141,\,\,3.141 \right)
For, 2π−θ2\pi -\theta :
2π−θ2\pi -\theta = 2 (3.141) – 10 = – 3.71 does not lie within (−π,  π)\left( -\pi ,\,\,\pi \right).
For, 2π+θ2\pi +\theta :
2π+θ2\pi +\theta = 2 (3.141) + 10 = 16.28 does not lie within (−π,  π)\left( -\pi ,\,\,\pi \right).
For, 4π−θ4\pi -\theta :
4π−θ4\pi -\theta = 4 (3.141) – 10 = 2.564, this lies within (−π,  π)\left( -\pi ,\,\,\pi \right).
Therefore, we can write cos (10) as cos (4π−104\pi -10).
Now, y=cos⁡−1[cos⁡(4π−10)]y={{\cos }^{-1}}\left[ \cos \left( 4\pi -10 \right) \right]
We get, y=4π−10y=4\pi -10........... (2)
Subtract equation (1) from equation (2), we get
y−x=(4π−10)−(3π−10) =4π−10−3π+10 =π\begin{aligned} & y-x=\left( 4\pi -10 \right)-\left( 3\pi -10 \right) \\\ & =4\pi -10-3\pi +10 \\\ & =\pi \end{aligned}
Hence, the value of y−xy-x is π\pi

Note: In this question, to determine the nature of the sign of the trigonometric functions when its angle is in which quadrant is important because the whole solution depends on it. Also, the even function means f(−x)=f(x)f\left( -x \right)=f\left( x \right) and odd functions are f(−x)=−f(x)f\left( -x \right)=-f\left( x \right).