Question

If $x=\cos 10{}^\circ \cos 20{}^\circ \cos 40{}^\circ$ , then the value of x is
(a) $\dfrac{1}{4}\tan 10{}^\circ$
(b) $\dfrac{1}{8}\cot 10{}^\circ$
(c) $\dfrac{1}{8}\cos 10{}^\circ$
(d) $\dfrac{1}{8}sec10{}^\circ$

Answer 1

Hint: Start by dividing and multiplying the right-hand side of the equation by $2\sin 10{}^\circ$ followed by the use of the formula of sin2A. Finally, use the property that trigonometric ratios are periodic functions and the knowledge of complementary angles related to trigonometric ratios to reach the answer.

Complete step-by-step answer:
Before moving to the solution, let us discuss the periodicity of sine and cosine function, which we would be using in the solution. All the trigonometric ratios, including sine and cosine, are periodic functions. We can better understand this using the graph of sine and cosine.
First, let us start with the graph of sinx.

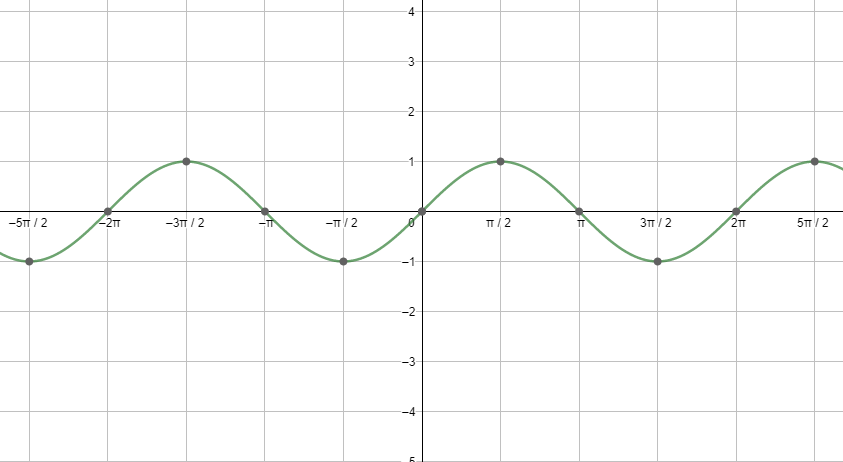
Next, let us see the graph of cosx.

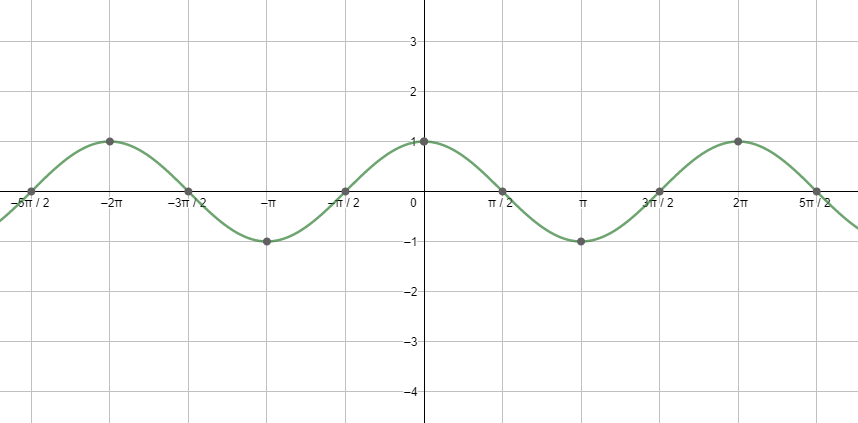
Looking at both the graphs, we can say that the graphs are repeating after a fixed period i.e. $2{{\pi }^{c}}$ . So, we can say that the fundamental period of the cosine function and the sine function is $2{{\pi }^{c}}=360{}^\circ$ . So, we can mathematically show it as:
$\sin (2{{\pi }^{c}}+x)=\sin (360{}^\circ +x)=\sin x$
$\cos (2{{\pi }^{c}}+x)=cos(360{}^\circ +x)=\cos x$
Also, some other results to remember are:
$\sin \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\sin (90{}^\circ -x)=\cos x$
$\cos \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\cos (90{}^\circ -x)=\sin x$
We will now solve the equation given in the question.
$\therefore x=\cos 10{}^\circ \cos 20{}^\circ \cos 40{}^\circ$
Now we will multiply and divide the right-hand side of the equation by $2\sin 10{}^\circ$ . On doing so, our equation becomes:
$x=\dfrac{2sin10{}^\circ \cos 10{}^\circ \cos 20{}^\circ \cos 40{}^\circ }{2\sin 10{}^\circ }$
We know sin2A=2sinAcosA, applying this to our equation, we get
$x=\dfrac{sin20{}^\circ \cos 20{}^\circ \cos 40{}^\circ }{2\sin 10{}^\circ }$
Now, dividing and multiplying the right-hand side of the equation by 2 and using the formula of sin2A, we get
$x=\dfrac{2sin20{}^\circ \cos 20{}^\circ \cos 40{}^\circ }{2\times 2\sin 10{}^\circ }$
$\Rightarrow x=\dfrac{sin40{}^\circ \cos 40{}^\circ }{4\sin 10{}^\circ }$
Again, dividing and multiplying the right-hand side of the equation by 2 and using the formula of sin2A, we get
$x=\dfrac{2\sin 40{}^\circ \cos 40{}^\circ }{2\times 4\sin 10{}^\circ }$
$\Rightarrow x=\dfrac{sin80{}^\circ }{8\sin 10{}^\circ }$
We know $\sin \left( \dfrac{{{\pi }^{c}}}{2}-x \right)=\sin (90{}^\circ -x)=\cos x$ , so, our equation becomes:
$x=\dfrac{sin\left( 90{}^\circ -10{}^\circ \right)}{8\sin 10{}^\circ }$
$\Rightarrow x=\dfrac{\cos 10{}^\circ }{8\sin 10{}^\circ }$
We know $\cot A=\dfrac{\cos A}{\sin A}$ , applying this to our expression, we get
$x=\dfrac{1}{8}\times \dfrac{\cos 10{}^\circ }{\sin 10{}^\circ }$
$x=\dfrac{1}{8}\cot 10{}^\circ$
Therefore, the answer to the above question is option (b).

Note: It is useful to remember the graph of the trigonometric ratios along with the signs of their values in different quadrants. For example: sine is always positive in the first and the second quadrant while negative in the other two. Also, remember the property of complementary angles of trigonometric ratios.