Question

If $X$ and $Y$ are two nonempty sets, where $f:X\to Y$ is function is defined such that $f(c)=\\{f(x):x\in C\\}$ for $C\subseteq X$ and ${{f}^{-1}}(D)=\\{x:f(x)\in D\\}$ for $D\subseteq Y$ , for any $A\subseteq Y$ and $B\subseteq Y$ then,
A). ${{f}^{-1}}\\{f(A)\\}=A$
B). ${{f}^{-1}}\\{f(A)\\}=\text{A only if f(X)=Y}$
C). $\text{f }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ =B only if B}\subseteq \text{f(x)}$
D). $\text{f }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ =B }$

Answer 1

First of all we will define $f$ and ${{f}^{-1}}$ in the two nonempty sets that is $X$ and $Y$ then by the figure $(1)$ we can determine that we cannot define $f(A)$ and $f(B)$ so we will define ${{f}^{-1}}(A)$ and ${{f}^{-1}}(B)$ after this check all the options to find which one is correct among them.

Complete step-by-step solution:
In mathematics the word set was first of all used by a German Mathematician George Cantor. He defined the set as follows: a set is any collection into a whole of definite and distinct objects of our intuition or thought.
The objects belonging to the set are called elements or members of the set.
A set containing no element is called the empty set. It is denoted by the symbol $\phi$
If $X$ and $Y$ are two nonempty sets
Here $f$ is defined as:
$\Rightarrow f:X\to Y$
Therefore the inverse of $f$ will be defined as:
$\Rightarrow {{f}^{-1}}:Y\to X$

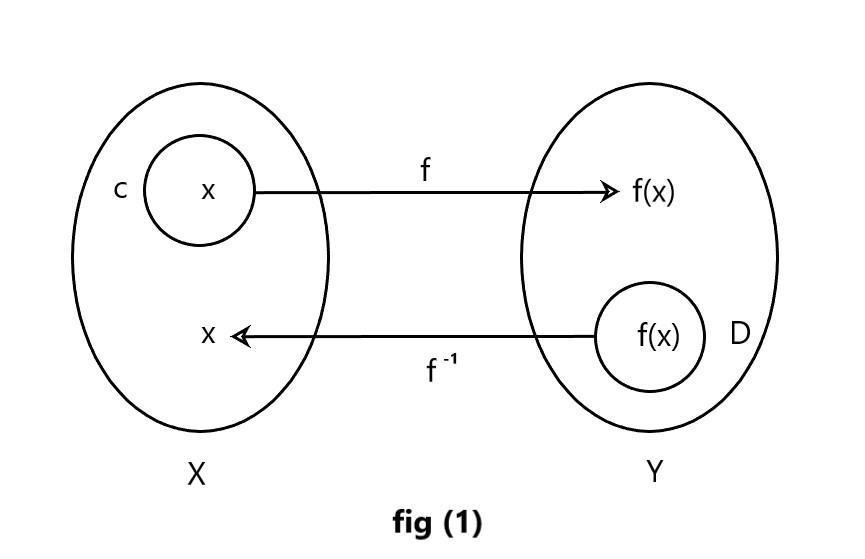
In the given figure $(1)$ we have given two sets $X$ and $Y$ and define $f$ from $X$ to $Y$
Take a set inside set $X$ and name it $C$ such that $C\subseteq X$ . Then take any value inside set $C$ name it $x$ such that image of $x$ comes in set $Y$ name it $f(x)$
If we define the inverse of these two sets in figure $(1)$ . Take a set inside set $Y$ name it $D$ and take any element inside the set $D$ and name it $f(x)$ such that image of $f(x)$ comes in set $X$ name it $x$ and the image is defined as ${{f}^{-1}}$
We have given that $A\subseteq Y$ and $B\subseteq Y$
Hence we cannot define $f(A)$ and $f(B)$ so we will define ${{f}^{-1}}(A)$ and ${{f}^{-1}}(B)$
Now we will check the given options:
In option $(1)$ ${{f}^{-1}}\\{f(A)\\}=A$ , $f(A)$ is defined hence this option is incorrect.
In option $(2)$ ${{f}^{-1}}\\{f(A)\\}=\text{A only if f(X)=Y}$ , $f(A)$ is defined hence this option is also incorrect.
In option $(3)$ $\text{f }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ =B only if B}\subseteq \text{f(x)}$
$\text{f }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ =B }$

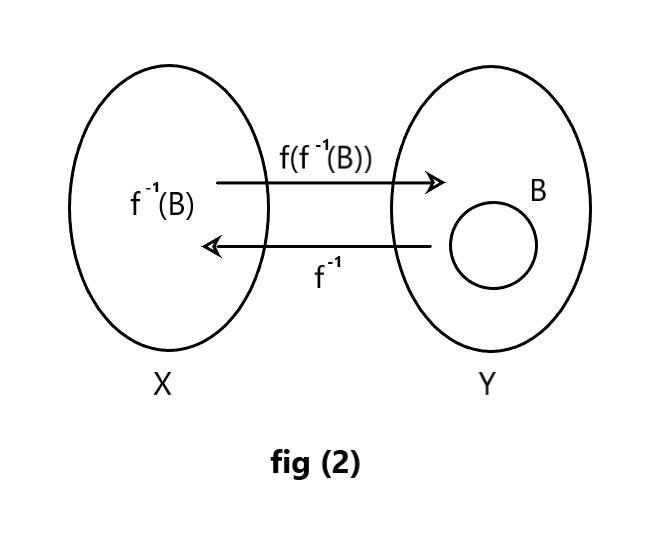
In figure $(2)$ you can see that you have given two sets $X$ and $Y$ let us take a set inside set $Y$ name it $B$ if we define ${{f}^{-1}}$ from $\text{B }$and the image will be ${{\text{f}}^{\text{-1}}}\text{(B)}$ if we again define ${{\text{f}}^{\text{-1}}}\text{(B)}$ through $\text{f}$ then the image will be defined as $\text{ }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ }$ and will belong to set $\text{B }$
Hence option $(3)$ is correct as $\text{f }\\!\\!\\{\\!\\!\text{ }{{\text{f}}^{\text{-1}}}\text{(B) }\\!\\!\\}\\!\\!\text{ =B }$ and $\text{B}\subseteq \text{f(x)}$ .

Note: If in any finite set, some elements are repeated then to find the cardinality of this set repeated elements counts only once, because repetition of elements is meaningless. For example: Let $A=\\{1,2,2,3,4,4,5\\}$ then clearly $n(A)=5$ .The number of distinct elements in a finite set is also called the order of a set.