Solveeit Logo
Login

Question

Question: If $x = a \sin 2\theta(1 + \cos 2\theta), y = b \cos 2\theta(1 - \cos 2\theta)$, then $\frac{dy}{dx}...

If x=asin⁡2θ(1+cos⁡2θ),y=bcos⁡2θ(1−cos⁡2θ)x = a \sin 2\theta(1 + \cos 2\theta), y = b \cos 2\theta(1 - \cos 2\theta), then dydx=\frac{dy}{dx} =

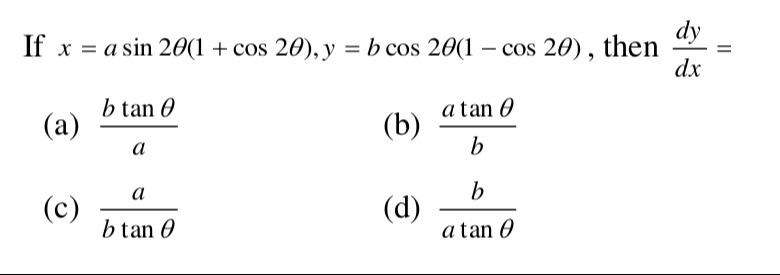
A

btan⁡θa\frac{b \tan \theta}{a}

B

atan⁡θb\frac{a \tan \theta}{b}

C

abtan⁡θ\frac{a}{b \tan \theta}

D

batan⁡θ\frac{b}{a \tan \theta}

Answer

btan⁡θa\frac{b \tan \theta}{a}

Explanation

Solution

Given the parametric equations: x=asin⁡2θ(1+cos⁡2θ)x = a \sin 2\theta(1 + \cos 2\theta) y=bcos⁡2θ(1−cos⁡2θ)y = b \cos 2\theta(1 - \cos 2\theta)

We need to find dydx=dy/dθdx/dθ\frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta}.

First, let's calculate dxdθ\frac{dx}{d\theta}. x=a(sin⁡2θ+sin⁡2θcos⁡2θ)x = a (\sin 2\theta + \sin 2\theta \cos 2\theta) Using the identity sin⁡Acos⁡B=12(sin⁡(A+B)+sin⁡(A−B))\sin A \cos B = \frac{1}{2}(\sin(A+B) + \sin(A-B)), or more simply sin⁡2θcos⁡2θ=12sin⁡(2θ+2θ)=12sin⁡4θ\sin 2\theta \cos 2\theta = \frac{1}{2} \sin(2\theta + 2\theta) = \frac{1}{2} \sin 4\theta. So, x=a(sin⁡2θ+12sin⁡4θ)x = a (\sin 2\theta + \frac{1}{2} \sin 4\theta).

Now, differentiate xx with respect to θ\theta: dxdθ=a(ddθ(sin⁡2θ)+12ddθ(sin⁡4θ))\frac{dx}{d\theta} = a \left( \frac{d}{d\theta}(\sin 2\theta) + \frac{1}{2} \frac{d}{d\theta}(\sin 4\theta) \right) dxdθ=a((2cos⁡2θ)+12(4cos⁡4θ))\frac{dx}{d\theta} = a \left( (2 \cos 2\theta) + \frac{1}{2} (4 \cos 4\theta) \right) dxdθ=a(2cos⁡2θ+2cos⁡4θ)\frac{dx}{d\theta} = a (2 \cos 2\theta + 2 \cos 4\theta) dxdθ=2a(cos⁡2θ+cos⁡4θ)\frac{dx}{d\theta} = 2a (\cos 2\theta + \cos 4\theta) Using the sum-to-product identity cos⁡A+cos⁡B=2cos⁡A+B2cos⁡A−B2\cos A + \cos B = 2 \cos \frac{A+B}{2} \cos \frac{A-B}{2}: cos⁡2θ+cos⁡4θ=2cos⁡2θ+4θ2cos⁡2θ−4θ2=2cos⁡3θcos⁡(−θ)=2cos⁡3θcos⁡θ\cos 2\theta + \cos 4\theta = 2 \cos \frac{2\theta + 4\theta}{2} \cos \frac{2\theta - 4\theta}{2} = 2 \cos 3\theta \cos (-\theta) = 2 \cos 3\theta \cos \theta. So, dxdθ=2a(2cos⁡3θcos⁡θ)=4acos⁡3θcos⁡θ\frac{dx}{d\theta} = 2a (2 \cos 3\theta \cos \theta) = 4a \cos 3\theta \cos \theta.

Alternatively, using the identities 1+cos⁡2θ=2cos⁡2θ1 + \cos 2\theta = 2 \cos^2 \theta and sin⁡2θ=2sin⁡θcos⁡θ\sin 2\theta = 2 \sin \theta \cos \theta: x=a(2sin⁡θcos⁡θ)(2cos⁡2θ)=4asin⁡θcos⁡3θx = a (2 \sin \theta \cos \theta)(2 \cos^2 \theta) = 4a \sin \theta \cos^3 \theta. Differentiate xx with respect to θ\theta using the product rule: dxdθ=4a(ddθ(sin⁡θ)cos⁡3θ+sin⁡θddθ(cos⁡3θ))\frac{dx}{d\theta} = 4a \left( \frac{d}{d\theta}(\sin \theta) \cos^3 \theta + \sin \theta \frac{d}{d\theta}(\cos^3 \theta) \right) dxdθ=4a((cos⁡θ)cos⁡3θ+sin⁡θ(3cos⁡2θ(−sin⁡θ)))\frac{dx}{d\theta} = 4a \left( (\cos \theta) \cos^3 \theta + \sin \theta (3 \cos^2 \theta (-\sin \theta)) \right) dxdθ=4a(cos⁡4θ−3sin⁡2θcos⁡2θ)\frac{dx}{d\theta} = 4a (\cos^4 \theta - 3 \sin^2 \theta \cos^2 \theta) dxdθ=4acos⁡2θ(cos⁡2θ−3sin⁡2θ)\frac{dx}{d\theta} = 4a \cos^2 \theta (\cos^2 \theta - 3 \sin^2 \theta) Using sin⁡2θ=1−cos⁡2θ\sin^2 \theta = 1 - \cos^2 \theta: dxdθ=4acos⁡2θ(cos⁡2θ−3(1−cos⁡2θ))=4acos⁡2θ(cos⁡2θ−3+3cos⁡2θ)=4acos⁡2θ(4cos⁡2θ−3)\frac{dx}{d\theta} = 4a \cos^2 \theta (\cos^2 \theta - 3(1 - \cos^2 \theta)) = 4a \cos^2 \theta (\cos^2 \theta - 3 + 3 \cos^2 \theta) = 4a \cos^2 \theta (4 \cos^2 \theta - 3). Using cos⁡2θ=2cos⁡2θ−1\cos 2\theta = 2\cos^2\theta - 1, so 2cos⁡2θ=1+cos⁡2θ2\cos^2\theta = 1+\cos 2\theta: 4cos⁡2θ−3=2(2cos⁡2θ)−3=2(1+cos⁡2θ)−3=2+2cos⁡2θ−3=2cos⁡2θ−14 \cos^2 \theta - 3 = 2(2\cos^2\theta) - 3 = 2(1+\cos 2\theta) - 3 = 2 + 2\cos 2\theta - 3 = 2\cos 2\theta - 1. So, dxdθ=4acos⁡2θ(2cos⁡2θ−1)\frac{dx}{d\theta} = 4a \cos^2 \theta (2 \cos 2\theta - 1).

Next, calculate dydθ\frac{dy}{d\theta}. y=b(cos⁡2θ−cos⁡22θ)y = b (\cos 2\theta - \cos^2 2\theta). Differentiate yy with respect to θ\theta: dydθ=b(ddθ(cos⁡2θ)−ddθ(cos⁡22θ))\frac{dy}{d\theta} = b \left( \frac{d}{d\theta}(\cos 2\theta) - \frac{d}{d\theta}(\cos^2 2\theta) \right) dydθ=b((−2sin⁡2θ)−(2cos⁡2θ⋅(−2sin⁡2θ)))\frac{dy}{d\theta} = b \left( (-2 \sin 2\theta) - (2 \cos 2\theta \cdot (-2 \sin 2\theta)) \right) dydθ=b(−2sin⁡2θ+4sin⁡2θcos⁡2θ)\frac{dy}{d\theta} = b (-2 \sin 2\theta + 4 \sin 2\theta \cos 2\theta) dydθ=2bsin⁡2θ(−1+2cos⁡2θ)\frac{dy}{d\theta} = 2b \sin 2\theta (-1 + 2 \cos 2\theta) dydθ=2bsin⁡2θ(2cos⁡2θ−1)\frac{dy}{d\theta} = 2b \sin 2\theta (2 \cos 2\theta - 1).

Now, calculate dydx=dy/dθdx/dθ\frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta}. dydx=2bsin⁡2θ(2cos⁡2θ−1)4acos⁡2θ(2cos⁡2θ−1)\frac{dy}{dx} = \frac{2b \sin 2\theta (2 \cos 2\theta - 1)}{4a \cos^2 \theta (2 \cos 2\theta - 1)}. Assuming 2cos⁡2θ−1≠02 \cos 2\theta - 1 \neq 0, we can cancel the term (2cos⁡2θ−1)(2 \cos 2\theta - 1). dydx=2bsin⁡2θ4acos⁡2θ\frac{dy}{dx} = \frac{2b \sin 2\theta}{4a \cos^2 \theta} Using the identity sin⁡2θ=2sin⁡θcos⁡θ\sin 2\theta = 2 \sin \theta \cos \theta: dydx=2b(2sin⁡θcos⁡θ)4acos⁡2θ\frac{dy}{dx} = \frac{2b (2 \sin \theta \cos \theta)}{4a \cos^2 \theta} dydx=4bsin⁡θcos⁡θ4acos⁡2θ\frac{dy}{dx} = \frac{4b \sin \theta \cos \theta}{4a \cos^2 \theta} dydx=bsin⁡θacos⁡θ\frac{dy}{dx} = \frac{b \sin \theta}{a \cos \theta} dydx=batan⁡θ\frac{dy}{dx} = \frac{b}{a} \tan \theta.

This matches option (a).