Solveeit Logo
Login

Question

Question: If $x = a \cos \theta$ and $y = b \sin \theta$, then $\left[ \frac{d^{2}y}{dx^{2}} \right]_{\theta =...

If x=acos⁡θx = a \cos \theta and y=bsin⁡θy = b \sin \theta, then [d2ydx2]θ=π4=\left[ \frac{d^{2}y}{dx^{2}} \right]_{\theta = \frac{\pi}{4}} =

A

−22(ba2)-2 \sqrt{2} \left( \frac{b}{a^{2}} \right)

B

2(a2b)\sqrt{2} \left( \frac{a^{2}}{b} \right)

C

22(ba2)2 \sqrt{2} \left( \frac{b}{a^{2}} \right)

D

2(a2b)2 \left( \frac{a^{2}}{b} \right)

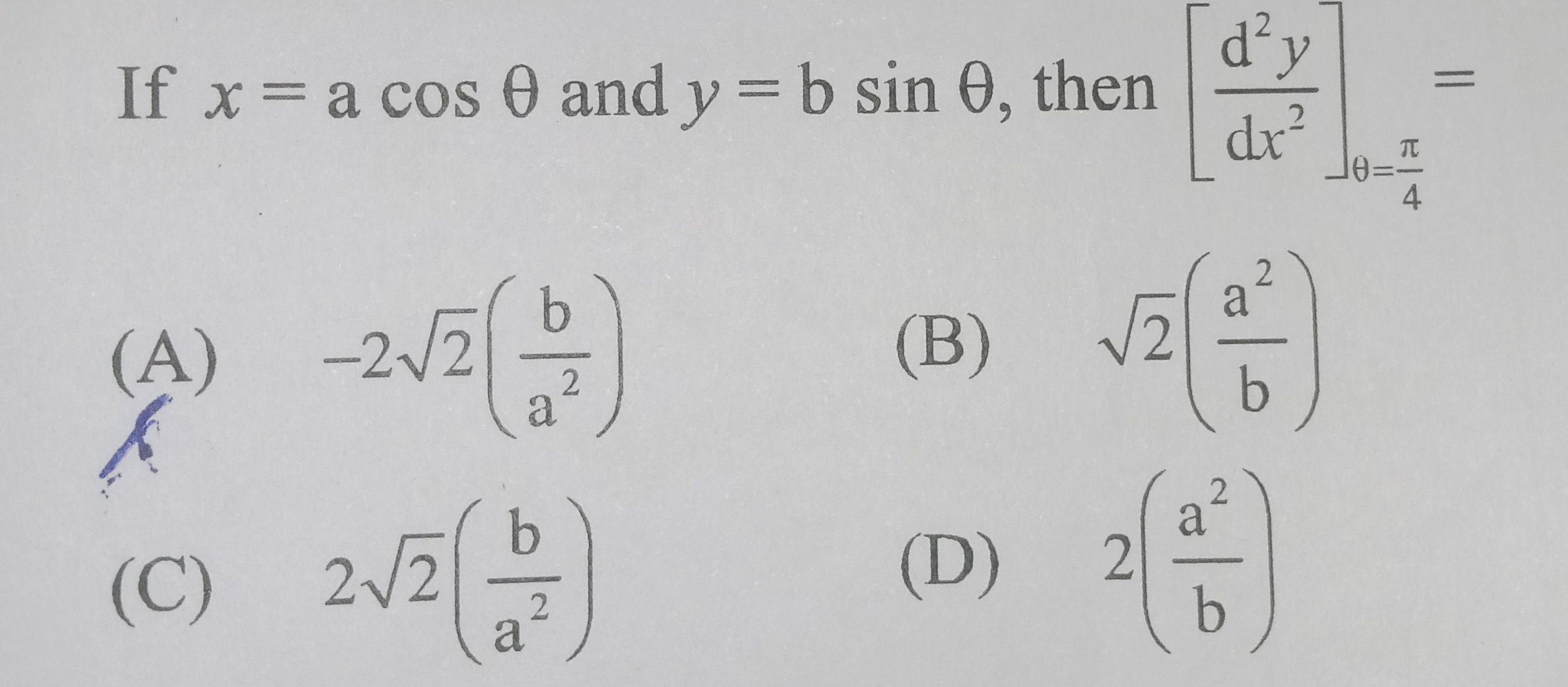
Answer

-2 \sqrt{2} \left( \frac{b}{a^{2}} \right)

Explanation

Solution

Given

x=acos⁡θ,y=bsin⁡θ.x = a\cos\theta,\quad y = b\sin\theta.

  1. First derivative:

    dxdθ=−asin⁡θ,dydθ=bcos⁡θ.\frac{dx}{d\theta} = -a\sin\theta,\quad \frac{dy}{d\theta} = b\cos\theta.

    Thus,

    dydx=dy/dθdx/dθ=bcos⁡θ−asin⁡θ=−bacot⁡θ.\frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta} = \frac{b\cos\theta}{-a\sin\theta} = -\frac{b}{a}\cot\theta.

  2. Second derivative: Differentiate dydx\frac{dy}{dx} with respect to θ\theta:

    ddθ(−bacot⁡θ)=−ba(−csc⁡2θ)=bacsc⁡2θ.\frac{d}{d\theta}\left(-\frac{b}{a}\cot\theta\right) = -\frac{b}{a}(-\csc^2\theta) = \frac{b}{a}\csc^2\theta.

    Now,

    d2ydx2=ddθ(dydx)dx/dθ=bacsc⁡2θ−asin⁡θ=−ba2csc⁡2θsin⁡θ.\frac{d^2y}{dx^2} = \frac{\frac{d}{d\theta}\left(\frac{dy}{dx}\right)}{dx/d\theta} = \frac{\frac{b}{a}\csc^2\theta}{-a\sin\theta} = -\frac{b}{a^2}\frac{\csc^2\theta}{\sin\theta}.

    Since csc⁡θ=1sin⁡θ\csc\theta = \frac{1}{\sin\theta}, it follows that:

    d2ydx2=−ba21sin⁡3θ.\frac{d^2y}{dx^2} = -\frac{b}{a^2}\frac{1}{\sin^3\theta}.

  3. At θ=π4\theta = \frac{\pi}{4}:

    sin⁡π4=22⇒sin⁡3π4=(22)3=228=24.\sin\frac{\pi}{4} = \frac{\sqrt2}{2}\quad \Rightarrow \quad \sin^3\frac{\pi}{4} = \left(\frac{\sqrt2}{2}\right)^3 = \frac{2\sqrt2}{8} = \frac{\sqrt2}{4}.

    Substitute to get:

    [d2ydx2]θ=π4=−ba2⋅1(2/4)=−ba2⋅42=−4ba22=−22 ba2.\left[\frac{d^2y}{dx^2}\right]_{\theta = \frac{\pi}{4}} = -\frac{b}{a^2}\cdot\frac{1}{\left(\sqrt2/4\right)} = -\frac{b}{a^2}\cdot\frac{4}{\sqrt2} = -\frac{4b}{a^2\sqrt2} = -\frac{2\sqrt2\,b}{a^2}.