Question

If x + 8y – 22 = 0, 5x + 2y – 34 = 0, 2x – 3y + 13 = 0 are three sides of triangle. Then the area of triangle is
$\begin{aligned} & \text{a) 36 square units}\text{.} \\\ & \text{b) 19 square units}\text{.} \\\ & \text{c) 42 square units}\text{.} \\\ & \text{d) 72 square units}\text{.} \\\ \end{aligned}$

Answer 1

Now we have equation of three lines, we will solve all of them simultaneously to find intersection points. These intersection points are nothing but the vertices of triangle. Now we know if $\left( {{x}_{1}},{{y}_{1}} \right)$ , $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ are vertices of triangle then the area of triangle is given by formula $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$

Complete step-by-step solution:
Now we have three equations
$x+8y-22=0.....................\left( 1 \right)$
$5x+2y-34=0..................\left( 2 \right)$
$2x-3y+13=0.................\left( 3 \right)$
First Let us draw a diagram for this triangle.

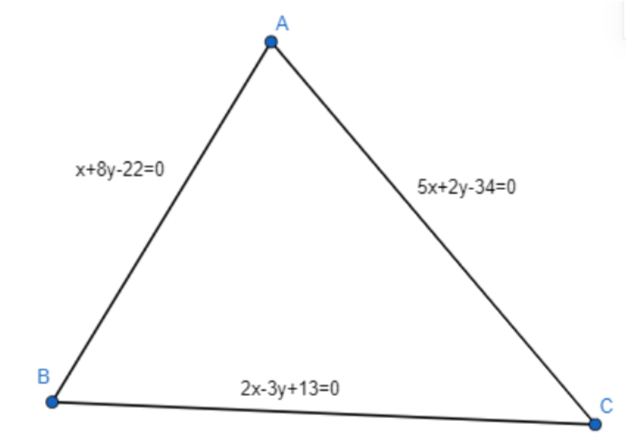
Now let us first find the coordinates of point A.
A is the intersection point is 5x + 2y – 34 = 0 and x + 8y – 22 = 0.
Now multiplying equation (1) by 5 and subtracting it from equation (2) we get.
$\begin{aligned} & 5x+2y-34-5x-40y+110=0 \\\ & \Rightarrow -38y+76=0 \\\ & \Rightarrow 38y=76 \\\ \end{aligned}$
Dividing the equation by 38 we get y = 2.
Now substituting y = 2 in equation (1) we get.

& \Rightarrow x+8\left( 2 \right)-22=0 \\\ & \Rightarrow x+16-22=0 \\\ & \Rightarrow x-6=0 \\\ & \therefore x=6 \\\ \end{aligned}$$ Now hence we get A = (6, 2)…………………….. (4) Now we will find the coordinates of point B. B is intersection of line x + 8y – 22 = 0 and 2x – 3y + 13 = 0 Now multiplying equation (1) by 2 and then subtracting it from equation (3) we get. $\begin{aligned} & \Rightarrow 2x-3y+13-2x-16y+44=0 \\\ & \Rightarrow -19y+57=0 \\\ & \Rightarrow 19y=57 \\\ \end{aligned}$ Now dividing the equation by 19 we get y = 3 Now substituting y = 3 in equation (1) we get $\begin{aligned} & \Rightarrow x+8\left( 3 \right)-22=0 \\\ & \Rightarrow x+24-22=0 \\\ & \Rightarrow x+2=0 \\\ & \therefore x=-2 \\\ \end{aligned}$ Hence we B = (-2, 3)……………………………………. (5) Now we will find the coordinates of point C C is the intersection point of lines 5x + 2y – 34 = 0 and 2x – 3y + 13 = 0 Now multiplying equation (2) by 3 and equation (3) by 2 and adding them we get $\begin{aligned} & 15x+6y-102+\left( 4x-6y+26 \right)=0 \\\ & \Rightarrow 15x+6y-102+4x-6y+26=0 \\\ & \Rightarrow 19x-76=0 \\\ & \Rightarrow 19x=76 \\\ \end{aligned}$ Dividing the equation by 19 we get x = 4. Now substituting x = 4 in (3) we get $\begin{aligned} & \Rightarrow 2\left( 4 \right)-3y+13=0 \\\ & \Rightarrow 8+13=3y \\\ & \Rightarrow 3y=21 \\\ \end{aligned}$ Now dividing the equation by 3 we get y = 7 Hence we have C = (4, 7)……………………. (6) Thus we have coordinates of point A, B, C. A = (6, 2) B = (-2, 3) and C = (4, 7) Now we know if $$\left( {{x}_{1}},{{y}_{1}} \right)$$ , $\left( {{x}_{2}},{{y}_{2}} \right)$ and $\left( {{x}_{3}},{{y}_{3}} \right)$ are vertices of triangle then the area of triangle is given by formula $\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|$ Hence we get area of triangle ABC = $\dfrac{1}{2}\left[ 6(3-7)+\left( -2 \right)\left( 7-2 \right)+4\left( 2-3 \right) \right]$ $\begin{aligned} & =\dfrac{1}{2}\left| 6(-4)+\left( -2 \right)\left( 5 \right)+4\left( -1 \right) \right| \\\ & =\dfrac{1}{2}\left| -24-10-4 \right| \\\ & =\dfrac{1}{2}\left| -38 \right| \\\ & =\dfrac{1}{2}\times 38=19 \\\ \end{aligned}$ Hence we have the area of triangle 19 square units. **Option b is the correct option.** **Note:** We can also find area of triangle by calculating distance between points. We know that distance between two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is given by $d=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$ Hence we can calculate the length of three sides of triangle and then we can use formula $A=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ to find area where $s=\dfrac{a+b+c}{2}$ and a, b, c are length of triangle.