Question

If $(x-2+\frac{1}{x})^{30} = n_0x^{30}+n_1x^{29}+......+n_{29}x+n_{30}+n_{31}x^{-1}+......+n_{60}x^{-30}$ and $C=n_0+n_1+n_2+......+n_{60}$.

Find the value of $(a+b)$ if $C-n_{30}=-\binom{a}{b}$.

[Note: $\binom{n}{r}$ denotes $^{n}C_{r}$.]

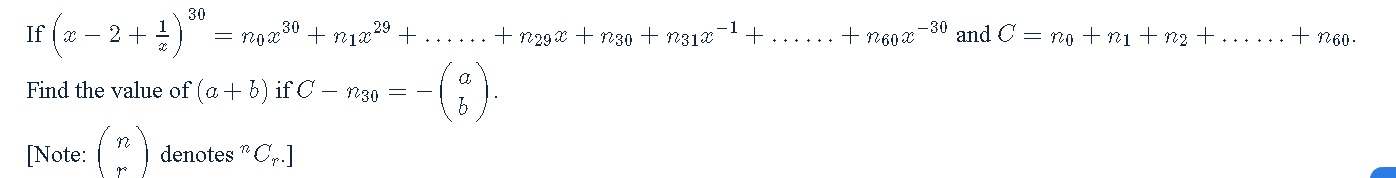
Answer 1

90

Answer 2

Solution

1. Sum of coefficients (C):

Substitute $x=1$ into the expansion: $C = \left(1-2+\frac{1}{1}\right)^{30} = (0)^{30} = 0.$

2. Finding $n_{30}$ (constant term coefficient):

Rewrite the expression: $x - 2 + \frac{1}{x} = \frac{x^2 - 2x + 1}{x} = \frac{(x-1)^2}{x}.$ Then, $\left(\frac{(x-1)^2}{x}\right)^{30} = \frac{(x-1)^{60}}{x^{30}}.$ The expansion of $(x-1)^{60}$ is: $(x-1)^{60} = \sum_{k=0}^{60} \binom{60}{k} (-1)^{60 - k} x^{k}.$ Multiplying by $x^{-30}$ gives: $\sum_{k=0}^{60} \binom{60}{k} (-1)^{60 - k} x^{k-30}.$ The constant term corresponds to $k-30=0$ or $k=30$: $n_{30} = \binom{60}{30} (-1)^{30} = \binom{60}{30}.$

3. Relating to the given expression:

We have, $C - n_{30} = 0 - \binom{60}{30} = -\binom{60}{30}.$ Comparing with $-\binom{a}{b}$, we get: $a = 60,\quad b = 30.$ Thus, $a+b = 60 + 30 = 90.$