Question

If work done by string on block A is W. shown in the given arrangement, then the work done by the string on block B is

(A) $- W$
(B) $\dfrac{{ - 2W}}{3}$
(C) $\dfrac{{2W}}{3}$
(D) $\dfrac{{ - 3W}}{2}$

Answer 1

The total length of the string is constant. The distance increase from the fixed point of one will result in a corresponding decrease in the other.
Formula used: In this solution we will be using the following formulae;
$W = Fd$ where $W$ is the work done by a force on a body, $F$ is the force acting on a body and $d$ is the distance moved by the body while the body acts on it.

Complete Step-by-Step Solution:

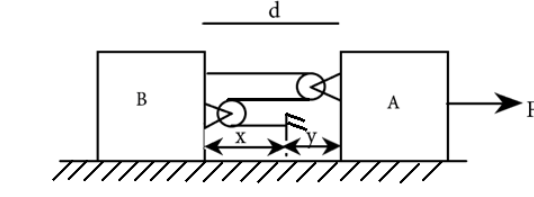
Let the distance between the two blocks be $d$. The let the distance of the left block to the fixed point be $x$, and the distance of the right block to fix point be $y$ such that their sum is the distance from each other
Hence, if the block A is pulled, then the distance $y$ changes. But since the total length of the string is constant, the distance $x$ must reduce correspondingly.
Then $\Delta y = - \Delta x$
Now, since it’s the same string, the tensions in each line of the string are all equal to say $T$. This means that the total tension acting on block A will be $2T$ (because the lines connected to A are 2).
Similarity, the tension on the block B will be $3T$
Work done on an object is $W = Fd$ where $F$ is the force acting on a body and $d$ is the distance moved by the body while the body acts on it.
Work done on A is
$W = 2T \times \Delta y$
$\Rightarrow \Delta y = \dfrac{W}{{2T}}$
Then the work done on B would be
$W = 3T \times \Delta x = 3T \times - \Delta y$
$\Rightarrow 3T \times - \left( {\dfrac{W}{{2T}}} \right) = - \dfrac{{3W}}{2}$

Hence the correct option is C

Note: For clarity, we can prove that $\Delta y = - \Delta x$ as follows.
The distance between the blocks is the sum of $x$ and $y$ as in
$d = x + y$
By finding the derivative (which gives the instantaneous change of the quantities), we get
$0 = dx + dy$ (since the length of the string is constant, the distance between the blocks cannot increase)
$dy= - dx$
$\Rightarrow \Delta y = - \Delta x$