Question

If we have the trigonometric function as $\sin A\ = \dfrac{1}{3}$ and $0 < A < 90$ then what is ${\cos A}$ ?

Answer 1

In this question, given that is $\sin\ A\ = \dfrac{1}{3}$ then we need to find ${\cos A}$. By using trigonometric identities and ratios, we can find the ${\cos A}$ . Also given a condition that $0 < A < 90$ . First we can consider a right angle triangle. With the help of Pythagoras theorem, we can find the adjacent side and can easily solve the problem.
Pythagoras theorem :
Pythagoras theorem deals with the relationship between the sides of the right angle triangle. It states that in a right angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
In a right angle triangle $ABC$,

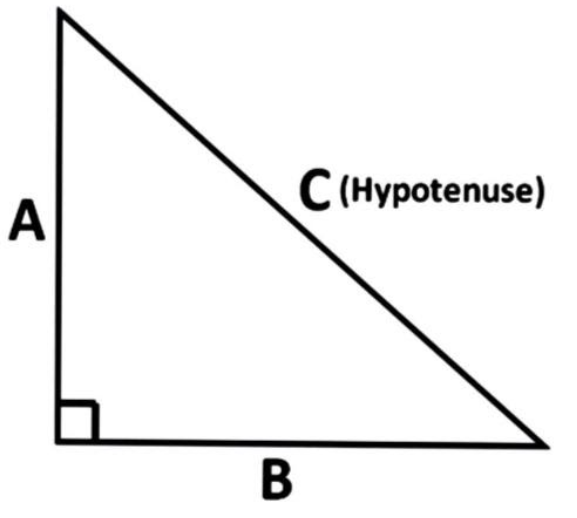
Where $C$ is the hypotenuse, $B$ is the base and $A$ is the perpendicular.
According to Pythagoras theorem,
$\left(\text{Hypotenuse} \right)^{2} = \left(\text{perpendicular} \right)^{2} + \left(\text{base} \right)^{2}$
$\Rightarrow {C}^{2} = A^{2} + B^{2}$
Formula used :
1.$\sin\theta = \dfrac{\text{Opposite side}}{\text{Hypotenuse}}$
2.$\cos\theta = \dfrac{\text{Adjacent side}}{\text{Hypotenuse}}$

Complete step-by-step solution:
Given,
$sin\ A\ = \dfrac{1}{3}$
We know that
$sin\theta = \dfrac{\text{opposite side}}{\text{Hypotenuse}}\$
Thus we get,
$\text{Opposite side} = 1$
$\text{Hypotenuse} = 3$
Let us consider a right angle triangle ${ABC}$,

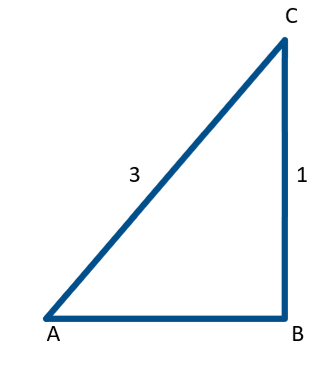
Here we need to find the adjacent side ${AB}$,
By Pythagoras theorem,
$BC^{2} = AB^{2} + AC^{2}$
By substituting the known values
We get,
$3^{2} = AB^{2} + 1^{2}$
By simplifying,
We get,
$AB^{2} = 9 – 1$
By subtracting,
We get,
$AB^{2} = 8$
On taking square root on both sides,
We get,
$AB = \sqrt{8}$
Thus we get, $AB = 2\sqrt{2}$
Therefore the adjacent side is $2\sqrt{2}$
Now we can find ${\cos A}$
We know that,
$\cos \theta = \dfrac{\text{Adjacent side}}{\text{Hypotenuse}}$
By substituting the values,
We get,
$\cos A = 2\dfrac{\sqrt{2}}{3}$
Thus we get the value of $\cos A = 2\dfrac{\sqrt{2}}{3}$
Final answer :
The value of $\cos A = 2\dfrac{\sqrt{2}}{3}$

Note: The concept used to solve the given problem is trigonometric identities and ratios. Trigonometric identities are nothing but they involve trigonometric functions including variables and constants. The common technique used in this problem is the Pythagoras theorem with the use of trigonometric functions.