Question

If we have a trigonometric expression as $\left[ 2\cos x \right]+\left[ \sin x \right]=-3$ then the range of the function $f\left( x \right)=\sin x+\sqrt{3}\cos x$ in $\left[ 0,2\pi \right]$ is (where $\left[ \cdot \right]$ denotes greatest integer function).

& A.\left( 2,-1 \right) \\\ & B.\left( -1,\dfrac{-1}{2} \right) \\\ & C.\left( -2,-1 \right) \\\ & D.\text{None of these} \\\ \end{aligned}$$

Answer 1

To solve this question, we will first find possible values of [2cosx] and [sinx] such that their sum is equal to -3 using the range of cosx and sinx which is [-1,1]. Using values of [2cosx] and [sinx] we will find the range of cosx and sinx in this sum. Using the range of cosx and sinx, we will find the range of x for both functions in $\left[ 0,2\pi \right]$ and then find a common range from both to get a range of x. At last, we will use the range of x to find the range of f(x).

Complete step-by-step solution
Here, we are given that $\left[ 2\cos x \right]+\left[ \sin x \right]=-3$.
As we know that, values of cosx and sinx lie between [-1,1] therefore to make the sum of $\left[ 2\cos x \right]+\left[ \sin x \right]$ as -3 we need the value of sinx as -1. Also the value of cosx will be -1. But the value of [2cosx] will be -2. Therefore,
$\left[ 2\cos x \right]=-2\text{ and }\left[ \sin x \right]=-1$.
Since we are dealing with the greatest integer here, the value of [2cosx] will be -2 if 2cosx will be anywhere between -2 and -1. (According to the definition of greatest integer). We cannot include -2, because we need value more than -2 and less than or equal to -1. Therefore, $-2\le 2\cos x < -1$.
Dividing by 2, $-1\le \cos x\text{ }<\text{ }\dfrac{-1}{2}$.
Since, we need range in $\left[ 0,2\pi \right]$ so let us draw graph of cosx in $\left[ 0,2\pi \right]$ which is given by,

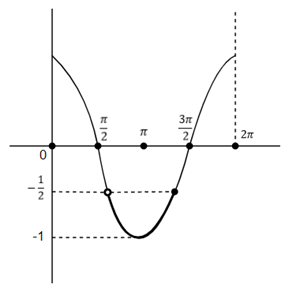
As we can see, the darker line in the graph is our required range, so the range will be between values of x when cosx is equal to $\dfrac{-1}{2}$ in $\left[ 0,2\pi \right]$.
We know that, $\cos \dfrac{2\pi }{3}=\cos \dfrac{4\pi }{3}=\dfrac{-1}{2}$ in $\left[ 0,2\pi \right]$.
Therefore, the range of x will be between $\dfrac{2\pi }{3}\text{ and }\dfrac{4\pi }{3}$.
Hence, for cosx $x\in \left( \dfrac{2\pi }{3},\dfrac{4\pi }{3} \right)$. (We cannot take $\cos \dfrac{2\pi }{3}\text{ and }\cos \dfrac{4\pi }{3}$ as these are equal to $\dfrac{-1}{2}$ which is not included).
Now, $\left[ \sin x \right]=-1$ means that sinx will be between 0 and -1. So sinx will be less than 0 and greater than or equal to -1. $\therefore -1\le \sin x\text{ }<\text{ }0$.
As we are dealing with negative values of sinx, we know that sinx is negative in the third and fourth quadrant, so the value of x will be between $\pi \text{ and }2\pi$.
Hence, sinx $x\in \left( \pi ,2\pi \right)$. We cannot include $\pi \text{ and }2\pi$ because $\sin \pi =\sin 2\pi =0$ and 0 is not included. Now, we need a common range of x.
Hence, taking intersection of $\left( \dfrac{2\pi }{3},\dfrac{4\pi }{3} \right)\text{ and }\left( \pi ,2\pi \right)$.

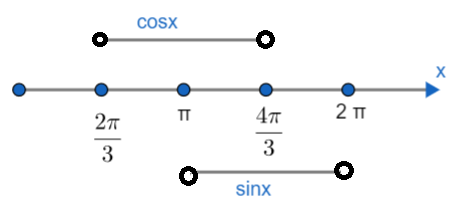
Region common to both will be $\left( \pi ,\dfrac{4\pi }{3} \right)$.
Hence, the range of x is $\left( \pi ,\dfrac{4\pi }{3} \right)$.
Now, we need to find the range of $f\left( x \right)=\sin x+\sqrt{3}\cos x$.
Let us first simplify f(x), $f\left( x \right)=\sin x+\sqrt{3}\cos x$.
Multiplying and dividing by 2, we get: $f\left( x \right)=2\left( \dfrac{1}{2}\sin x+\dfrac{\sqrt{3}}{2}\cos x \right)$.
As we know, $\cos \dfrac{\pi }{6}=\dfrac{\sqrt{3}}{2}\text{ and }\sin \dfrac{\pi }{6}=\dfrac{1}{2}$ so we get: $f\left( x \right)=2\left( \sin \dfrac{\pi }{6}\sin x+\cos x\cos \dfrac{\pi }{6} \right)$.
Now function becomes of the form $\sin A\sin B+ \cos A\cos B$. We know that, $\cos \left( A-B \right)=\sin A\sin B+ \cos A\cos B$ so we get:
$f\left( x \right)=2\left( \cos \left( x-\dfrac{\pi }{6} \right) \right)$.
Now, let us find the range of $2\left( \cos \left( x-\dfrac{\pi }{6} \right) \right)$.
Since the range of x is $\left( \pi ,\dfrac{4\pi }{3} \right)$.
So we can write it as $\pi \text{ }<\text{ }x\text{ }<\text{ }\dfrac{4\pi }{3}$.
Subtracting $\dfrac{\pi }{6}$ we get:
$\begin{aligned} & \pi -\dfrac{\pi }{6}\text{ }<\text{ }x-\dfrac{\pi }{6}\text{ }<\text{ }\dfrac{4\pi }{3}-\dfrac{\pi }{6} \\\ & \Rightarrow \dfrac{5\pi }{6}\text{ }<\text{ }\dfrac{x-\pi }{6}\text{ }<\text{ }\dfrac{7\pi }{6} \\\ \end{aligned}$.
Now to take value of $\cos \left( x-\dfrac{\pi }{6} \right)$ let us look at graph,

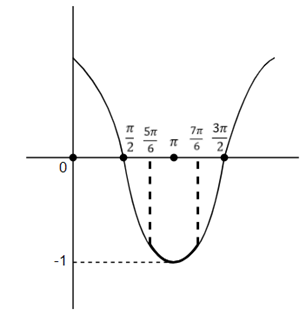
Hence, our range will be the darker part, since the minimum value will be -1 so $\cos \left( x-\dfrac{\pi }{6} \right)\ge -1$.
Also the minimum value will be either $\cos \left( \dfrac{5\pi }{6} \right),\cos \left( \dfrac{7\pi }{6} \right)$.
Let us evaluate them,
$\begin{aligned} & \cos \left( \dfrac{5\pi }{6} \right)=\cos \left( \pi -\dfrac{\pi }{6} \right)=\dfrac{-\cos \pi }{6}=\dfrac{-\sqrt{3}}{2} \\\ & \Rightarrow \cos \left( \dfrac{7\pi }{6} \right)=\cos \left( \pi +\dfrac{\pi }{6} \right)=\dfrac{-\cos \pi }{6}=\dfrac{-\sqrt{3}}{2} \\\ \end{aligned}$
So the maximum value of $\dfrac{-\sqrt{3}}{2}$.
Hence $\cos \left( x-\dfrac{\pi }{6} \right)\text{ }<\text{ }\dfrac{-\sqrt{3}}{2}$. (We cannot take value of $\cos \left( \dfrac{5\pi }{6} \right),\cos \left( \dfrac{7\pi }{6} \right)$ in range because of open bracket)
Hence $-1\le \cos \left( x-\dfrac{\pi }{6} \right)\text{ }<\text{ }\dfrac{-\sqrt{3}}{2}$.
Multiplying by 2, $-2\le 2\cos \left( x-\dfrac{\pi }{6} \right)\text{ }<\text{ }-\sqrt{3}$.
Since $f\left( x \right)=2\cos \left( x-\dfrac{\pi }{6} \right)$ so, $-2\le f\left( x \right)\text{ }<\text{ }-\sqrt{3}$.
Hence the range of f(x) is $\left[ -2,-\sqrt{3} \right)$.
Hence, none of the options are correct.
So option D is the correct answer.

Note: Students should note that the greatest integer (x) rounds down a real number to the nearest integer. Here x could be less than or equal to ${{x}_{7}}$. Students should always draw graphs for calculating range. They should keep in mind all the trigonometric formulas before solving the sum. Take care of open and closed intervals.