Question
Question: If \[{{W}_{1}},{{W}_{2}}\text{ and }{{W}_{3}}\] represent the work done in moving a particle from A ...
If W1,W2 and W3 represent the work done in moving a particle from A to B along three different paths 1, 2 and 3 respectively (as shown) in a gravitational field of point mass m, then find the correct relation between W1,W2 and W3.
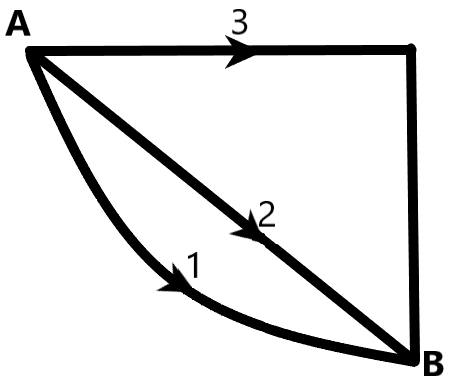
Solution
We need to understand the path dependence of the given physical parameter, here the gravitational field to recognize the relation between the work done by the field against the movement of the particle through all of the given paths.
Complete step-by-step answer:
We are given the paths of motion of a particle of mass ‘m’ in a gravitational field between two fixed points A and B. We know that the gravitational field is the field in which a body of certain mass experiences an attractive force due to another body of certain mass. The gravitational force is dependent on the mass of the body exerting the force and the inversely proportional to the square of the distance between two bodies. It is given as –
GF=R2GM
The distance between the two bodies is the straight line connecting these bodies. So, between any two points the field will be constant independent of the path taken to reach the other point.
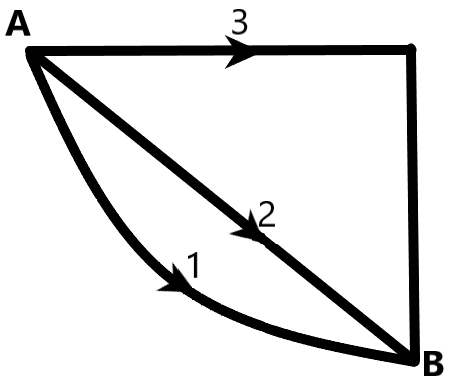
From the above explanation, we understand that the gravitational field is conservative in nature. The field is independent of the paths taken by a body in it to move from a point A to the point B.
Therefore, we can conclude that the work done in moving the particle from A to B is the same independent of the paths 1, 2 and 3. All the work done in the same field is equal.
∴W1=W2=W3
This is the required solution.
Note: The conservative forces are those forces for which the work done in moving a particle from one point to the other is independent of the path taken. The electrostatic forces, the gravitational forces and the magnetostatic forces are examples.
