Question

If vertices of an ellipse are ${\text{( - 4,1),(6,1)}}$and ${\text{x - 2y = 2}}$is a focal chord, then the equation of ellipse is
A) $\dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{{{\text{16}}}}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{{{\text{25}}}}{\text{ = 1}}$
B) $\dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{{25}}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{{16}}{\text{ = 1}}$
C) $\dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{{25}}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{9}{\text{ = 1}}$
D) $\dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{9}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{{25}}{\text{ = 1}}$

Answer 1

Use the concept that the length of the major axis is ${\text{2a}}$. And then the focal chord will pass through the focal point so let the focal point be ${\text{(ae,0)}}$. As a is known and so calculate b, as ${\text{e = }}\sqrt {{\text{1 - }}\dfrac{{{{\text{b}}^{\text{2}}}}}{{{{\text{a}}^{\text{2}}}}}}$ and hence from here b can be calculated. Use the general equation of ellipse which is given as $\dfrac{{{{\text{x}}^{\text{2}}}}}{{{{\text{a}}^{\text{2}}}}}{\text{ + }}\dfrac{{{{\text{y}}^{\text{2}}}}}{{{{\text{b}}^{\text{2}}}}}{\text{ = 1}}$, for centre${\text{(0,0)}}$. Thus, the equation can be obtained.

Complete step by step solution: As per the given the vertex of ellipse are ${\text{( - 4,1),(6,1)}}$ and the focal chord is given as ${\text{x - 2y = 2}}$,
Let, $({x_1},{y_1}) = (6,1)$ and $({x_2},{y_2}) = ( - 4,1)$
Diagram:

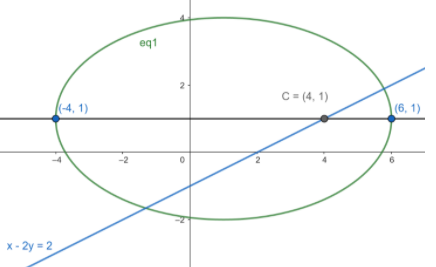
As per the diagram we can see that the length of major axis given here is ${\text{2a}}$which is equal to$({x_1} - {x_2}) = (6 - ( - 4)) = 10$.
So,

$${\text{2a = 10}} \\\ \Rightarrow {\text{a = 5}} \\\$$

Here we can calculate the centre of ellipse as both the vertices are known, which are$({x_1},{y_1}) = (6,1)$ and $({x_2},{y_2}) = ( - 4,1)$
So we use the section formula to calculate the centre of ellipse,
$\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
On substituting the values $({x_1},{y_1}) = (6,1)$ and $({x_2},{y_2}) = ( - 4,1)$ we get,

$$\Rightarrow (\dfrac{{6 - 4}}{2},\dfrac{{1 + 1}}{2}{\text{)}} \\\ \Rightarrow (\dfrac{2}{2},\dfrac{2}{2}) \\\ \Rightarrow (1,1) \\\$$

And so the focal point of the ellipse can be given as ${\text{(ae,1)}}$,which will satisfy the focal chord ${\text{x - 2y = 2}}$
$\therefore {\text{x - 2y = 2}}$
On substituting the point ${\text{(ae,1)}}$, we get,
$\Rightarrow {\text{ae - 2(1) = 2}}$
On simplification we get,
$\Rightarrow {\text{ae = 4}}$
Now as ${\text{a = 5}}$,
$\Rightarrow {\text{e = }}\dfrac{4}{5}$
Hence, as we know the value of e, now calculate b using the formula ${\text{e = }}\sqrt {{\text{1 - }}\dfrac{{{{\text{b}}^{\text{2}}}}}{{{{\text{a}}^{\text{2}}}}}}$
On substituting values of e and a we get,
$\Rightarrow \dfrac{{\text{4}}}{{\text{5}}}{\text{ = }}\sqrt {{\text{1 - }}\dfrac{{{{\text{b}}^{\text{2}}}}}{{{5^{\text{2}}}}}}$
On squaring both the sides we get,
$\Rightarrow \dfrac{{{\text{16}}}}{{{\text{25}}}}{\text{ = 1 - }}\dfrac{{{{\text{b}}^{\text{2}}}}}{{{\text{25}}}}$
On rearranging we get,
$\Rightarrow \dfrac{{{{\text{b}}^{\text{2}}}}}{{{\text{25}}}}{\text{ = 1 - }}\dfrac{{{\text{16}}}}{{{\text{25}}}}$
On simplification we get,
$\Rightarrow \dfrac{{{{\text{b}}^{\text{2}}}}}{{{\text{25}}}}{\text{ = }}\dfrac{{\text{9}}}{{{\text{25}}}}$
On further simplification of the above equation we get,
$\Rightarrow {{\text{b}}^{\text{2}}}{\text{ = 9}}$
On taking positive square root we get,
$\Rightarrow {\text{b = 3}}$
Hence, as we know the values of a and b and centre,and the equation of ellipse is $\dfrac{{{{{\text{(x - h)}}}^{\text{2}}}}}{{{a^{\text{2}}}}}{\text{ + }}\dfrac{{{{{\text{(y - k)}}}^{\text{2}}}}}{{{b^{\text{2}}}}}{\text{ = 1}}$, where (h,k) is centre,
On substituting the values of ${\text{a = 5}}$,${\text{b = 3}}$and centre as (1,1), we get,

$$\Rightarrow \dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{{{5^{\text{2}}}}}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{{{3^{\text{2}}}}}{\text{ = 1}} \\\ \Rightarrow \dfrac{{{{{\text{(x - 1)}}}^{\text{2}}}}}{{25}}{\text{ + }}\dfrac{{{{{\text{(y - 1)}}}^{\text{2}}}}}{9}{\text{ = 1}} \\\$$

Hence, option (c) is our required correct answer.

Note: You should always first draw the diagram and then proceed further to solve the question and proper calculations should be done.
An ellipse is a plane curve surrounding two focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. As such, it generalizes a circle, which is the special type of ellipse in which the two focal points are the same.
Or
A plane curve whose sums of the distances of each point in its periphery from two fixed points, the foci, are always equal. It is a conic section formed by the intersection of a right circular cone by a plane that cuts the axis and the surface of the cone.