Question

If velocity of a satellite is half of escape velocity, then distance of the satellite from earth surface will be –
A) 6400 km
B) 12800 km
C) 6400$\sqrt{2}$km
D) $\dfrac{6400}{\sqrt{2}}$km

Answer 1

We need to find the formulae for the escape velocity of an object from the earth and the velocity of a satellite in an orbit of the earth. From those formulas we can relate the required distance from the earth to the satellite in this case.

Complete answer:
We know that the escape velocity of a planet is defined as the minimum velocity required for an object within the gravitational field of the planet to escape into space. It is dependent on the radius of the planet, the mass of the planet and the gravitational constant ‘G’. The escape velocity is given as –
${{v}_{e}}=\sqrt{\dfrac{2GM}{R}}$
Where, M is the mass of the planet and R is the radius of the planet.

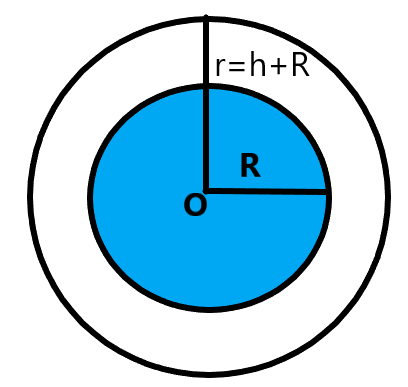
Now, we know that an object which is revolving around a planet within the gravitational field of the planet is supposed to have a maximum velocity beyond which the object will get thrown into the space. This is balanced by the gravitational force offered by the planet and the centripetal force of revolution. We define it as the orbital velocity of the satellite. We can write it as –
${{v}_{o}}=\sqrt{\dfrac{GM}{r}}$
Where, r is the distance between the center of the planet and the satellite.
From the above two relations, we can get the relation between the ‘r’ and the ‘R’ for the planet earth.
It is given that the orbital velocity of the satellite is half the escape velocity.
If the distance from the surface to the satellite is ‘h’ and the radius of the earth is 6400km. Then,

& {{v}_{o}}=\dfrac{{{v}_{e}}}{2} \\\ & \Rightarrow \sqrt{\dfrac{GM}{r}}=\dfrac{1}{2}\sqrt{\dfrac{2GM}{R}} \\\ \end{aligned}$$ $$\begin{aligned} & \Rightarrow r=2R \\\ & \text{but, }r=h+R \\\ & \therefore h=R=6400km \\\ \end{aligned}$$ This is the required solution. **The correct answer is option A.** **Note:** The kinetic energy of a satellite needs to be reduced as it moves from a nearer orbit to a farer orbit in order to keep the satellite in orbit. The velocity of the satellite moving around the planet is lowered in order to achieve this criterion as they are related directly.