Solveeit Logo
Login

Question

Question: If $\vec{a}$ and $\vec{b}$ are vectors such that $|\vec{a}|=2$, $|\vec{b}|=1$, $\vec{a}\^\vec{b}=\fr...

If a⃗\vec{a} and b⃗\vec{b} are vectors such that ∣a⃗∣=2|\vec{a}|=2, ∣b⃗∣=1|\vec{b}|=1, \vec{a}\^\vec{b}=\frac{\pi}{3} and c⃗\vec{c} satisfies 2(a⃗+b⃗)+c⃗=b⃗×c⃗2(\vec{a}+\vec{b})+\vec{c}=\vec{b}\times\vec{c}, then the value of ∣(a⃗×c⃗).b⃗∣|(\vec{a}\times\vec{c}).\vec{b}| is -

A

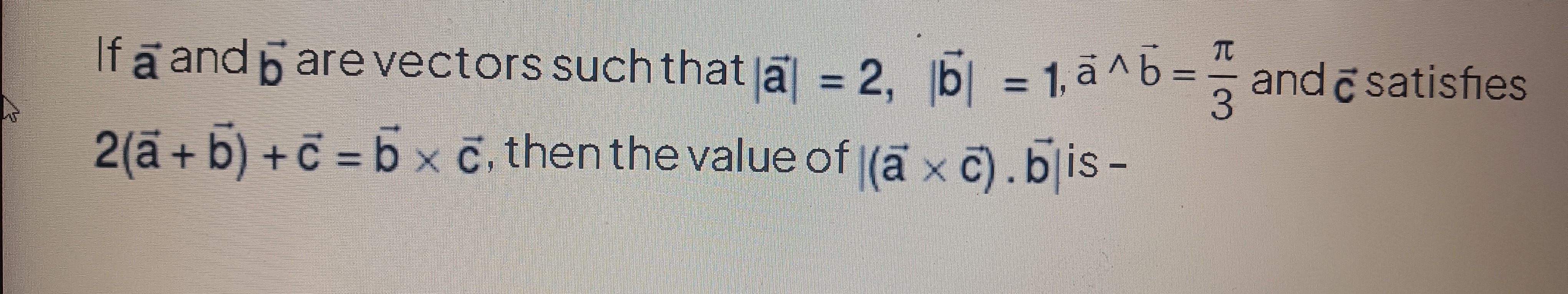
0

B

1

C

2

D

3

Answer

3

Explanation

Solution

The problem asks for ∣(a⃗×c⃗).b⃗∣|(\vec{a}\times\vec{c}).\vec{b}|, which is the absolute value of the scalar triple product ∣[a⃗,c⃗,b⃗]∣|[\vec{a}, \vec{c}, \vec{b}]|. By the properties of the scalar triple product, ∣[a⃗,c⃗,b⃗]∣=∣[a⃗,b⃗,c⃗]∣|[\vec{a}, \vec{c}, \vec{b}]| = |[\vec{a}, \vec{b}, \vec{c}]|.

Given: ∣a⃗∣=2|\vec{a}|=2, ∣b⃗∣=1|\vec{b}|=1, and the angle between a⃗\vec{a} and b⃗\vec{b} is π3\frac{\pi}{3}. The dot product a⃗⋅b⃗=∣a⃗∣∣b⃗∣cos⁡(π3)=(2)(1)(12)=1\vec{a}\cdot\vec{b} = |\vec{a}||\vec{b}|\cos(\frac{\pi}{3}) = (2)(1)(\frac{1}{2}) = 1.

The given vector equation is 2(a⃗+b⃗)+c⃗=b⃗×c⃗2(\vec{a}+\vec{b})+\vec{c}=\vec{b}\times\vec{c}. This can be written as 2a⃗+2b⃗+c⃗=b⃗×c⃗2\vec{a} + 2\vec{b} + \vec{c} = \vec{b}\times\vec{c}. Taking the dot product with b⃗\vec{b}: (2a⃗+2b⃗+c⃗)⋅b⃗=(b⃗×c⃗)⋅b⃗(2\vec{a} + 2\vec{b} + \vec{c}) \cdot \vec{b} = (\vec{b}\times\vec{c}) \cdot \vec{b}. Since (b⃗×c⃗)⋅b⃗=0(\vec{b}\times\vec{c}) \cdot \vec{b} = 0, we have: 2a⃗⋅b⃗+2b⃗⋅b⃗+c⃗⋅b⃗=02\vec{a}\cdot\vec{b} + 2\vec{b}\cdot\vec{b} + \vec{c}\cdot\vec{b} = 0. Substituting known values: 2(1)+2(∣b⃗∣2)+c⃗⋅b⃗=02(1) + 2(|\vec{b}|^2) + \vec{c}\cdot\vec{b} = 0. 2+2(12)+c⃗⋅b⃗=0  ⟹  4+c⃗⋅b⃗=0  ⟹  c⃗⋅b⃗=−42 + 2(1^2) + \vec{c}\cdot\vec{b} = 0 \implies 4 + \vec{c}\cdot\vec{b} = 0 \implies \vec{c}\cdot\vec{b} = -4.

Let c⃗=c⃗∥+c⃗⊥\vec{c} = \vec{c}_{\parallel} + \vec{c}_{\perp}, where c⃗∥\vec{c}_{\parallel} is parallel to b⃗\vec{b} and c⃗⊥\vec{c}_{\perp} is perpendicular to b⃗\vec{b}. c⃗∥=(c⃗⋅b^)b^=(c⃗⋅b⃗)b⃗\vec{c}_{\parallel} = (\vec{c}\cdot\hat{b})\hat{b} = (\vec{c}\cdot\vec{b})\vec{b} (since ∣b⃗∣=1|\vec{b}|=1). So, c⃗∥=−4b⃗\vec{c}_{\parallel} = -4\vec{b}. Thus, c⃗=−4b⃗+c⃗⊥\vec{c} = -4\vec{b} + \vec{c}_{\perp}.

Substitute this into the original vector equation: 2a⃗+2b⃗+(−4b⃗+c⃗⊥)=b⃗×(−4b⃗+c⃗⊥)2\vec{a} + 2\vec{b} + (-4\vec{b} + \vec{c}_{\perp}) = \vec{b}\times(-4\vec{b} + \vec{c}_{\perp}). 2a⃗−2b⃗+c⃗⊥=−4(b⃗×b⃗)+b⃗×c⃗⊥2\vec{a} - 2\vec{b} + \vec{c}_{\perp} = -4(\vec{b}\times\vec{b}) + \vec{b}\times\vec{c}_{\perp}. Since b⃗×b⃗=0⃗\vec{b}\times\vec{b} = \vec{0}, we get 2a⃗−2b⃗+c⃗⊥=b⃗×c⃗⊥2\vec{a} - 2\vec{b} + \vec{c}_{\perp} = \vec{b}\times\vec{c}_{\perp}.

Now, we want to find [a⃗,b⃗,c⃗]=[a⃗,b⃗,−4b⃗+c⃗⊥][\vec{a}, \vec{b}, \vec{c}] = [\vec{a}, \vec{b}, -4\vec{b} + \vec{c}_{\perp}]. Using linearity: [a⃗,b⃗,−4b⃗]+[a⃗,b⃗,c⃗⊥][\vec{a}, \vec{b}, -4\vec{b}] + [\vec{a}, \vec{b}, \vec{c}_{\perp}]. Since [a⃗,b⃗,b⃗]=0[\vec{a}, \vec{b}, \vec{b}] = 0, this simplifies to [a⃗,b⃗,c⃗⊥][\vec{a}, \vec{b}, \vec{c}_{\perp}].

From 2a⃗−2b⃗+c⃗⊥=b⃗×c⃗⊥2\vec{a} - 2\vec{b} + \vec{c}_{\perp} = \vec{b}\times\vec{c}_{\perp}, take the dot product with a⃗\vec{a}: (2a⃗−2b⃗+c⃗⊥)⋅a⃗=(b⃗×c⃗⊥)⋅a⃗(2\vec{a} - 2\vec{b} + \vec{c}_{\perp}) \cdot \vec{a} = (\vec{b}\times\vec{c}_{\perp}) \cdot \vec{a}. 2∣a⃗∣2−2a⃗⋅b⃗+a⃗⋅c⃗⊥=[a⃗,b⃗,c⃗⊥]2|\vec{a}|^2 - 2\vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c}_{\perp} = [\vec{a}, \vec{b}, \vec{c}_{\perp}]. 2(22)−2(1)+a⃗⋅c⃗⊥=[a⃗,b⃗,c⃗⊥]2(2^2) - 2(1) + \vec{a}\cdot\vec{c}_{\perp} = [\vec{a}, \vec{b}, \vec{c}_{\perp}]. 8−2+a⃗⋅c⃗⊥=[a⃗,b⃗,c⃗⊥]  ⟹  6+a⃗⋅c⃗⊥=[a⃗,b⃗,c⃗⊥]8 - 2 + \vec{a}\cdot\vec{c}_{\perp} = [\vec{a}, \vec{b}, \vec{c}_{\perp}] \implies 6 + \vec{a}\cdot\vec{c}_{\perp} = [\vec{a}, \vec{b}, \vec{c}_{\perp}].

Consider the magnitude squared of 2a⃗−2b⃗+c⃗⊥=b⃗×c⃗⊥2\vec{a} - 2\vec{b} + \vec{c}_{\perp} = \vec{b}\times\vec{c}_{\perp}. ∣b⃗×c⃗⊥∣=∣b⃗∣∣c⃗⊥∣sin⁡(π2)=(1)∣c⃗⊥∣(1)=∣c⃗⊥∣|\vec{b}\times\vec{c}_{\perp}| = |\vec{b}||\vec{c}_{\perp}|\sin(\frac{\pi}{2}) = (1)|\vec{c}_{\perp}|(1) = |\vec{c}_{\perp}|. So, ∣2a⃗−2b⃗+c⃗⊥∣2=∣c⃗⊥∣2|2\vec{a} - 2\vec{b} + \vec{c}_{\perp}|^2 = |\vec{c}_{\perp}|^2. (2a⃗−2b⃗+c⃗⊥)⋅(2a⃗−2b⃗+c⃗⊥)=∣c⃗⊥∣2(2\vec{a} - 2\vec{b} + \vec{c}_{\perp})\cdot(2\vec{a} - 2\vec{b} + \vec{c}_{\perp}) = |\vec{c}_{\perp}|^2. ∣2a⃗−2b⃗∣2+∣c⃗⊥∣2+2(2a⃗−2b⃗)⋅c⃗⊥=∣c⃗⊥∣2|2\vec{a} - 2\vec{b}|^2 + |\vec{c}_{\perp}|^2 + 2(2\vec{a} - 2\vec{b})\cdot\vec{c}_{\perp} = |\vec{c}_{\perp}|^2. ∣2a⃗−2b⃗∣2+2(2a⃗⋅c⃗⊥−2b⃗⋅c⃗⊥)=0|2\vec{a} - 2\vec{b}|^2 + 2(2\vec{a}\cdot\vec{c}_{\perp} - 2\vec{b}\cdot\vec{c}_{\perp}) = 0. ∣2a⃗−2b⃗∣2=(2a⃗−2b⃗)⋅(2a⃗−2b⃗)=4∣a⃗∣2−8a⃗⋅b⃗+4∣b⃗∣2=4(4)−8(1)+4(1)=16−8+4=12|2\vec{a} - 2\vec{b}|^2 = (2\vec{a}-2\vec{b})\cdot(2\vec{a}-2\vec{b}) = 4|\vec{a}|^2 - 8\vec{a}\cdot\vec{b} + 4|\vec{b}|^2 = 4(4) - 8(1) + 4(1) = 16 - 8 + 4 = 12. Since b⃗⋅c⃗⊥=0\vec{b}\cdot\vec{c}_{\perp} = 0: 12+2(2a⃗⋅c⃗⊥−0)=0  ⟹  12+4a⃗⋅c⃗⊥=0  ⟹  a⃗⋅c⃗⊥=−312 + 2(2\vec{a}\cdot\vec{c}_{\perp} - 0) = 0 \implies 12 + 4\vec{a}\cdot\vec{c}_{\perp} = 0 \implies \vec{a}\cdot\vec{c}_{\perp} = -3.

Substitute a⃗⋅c⃗⊥=−3\vec{a}\cdot\vec{c}_{\perp} = -3 into 6+a⃗⋅c⃗⊥=[a⃗,b⃗,c⃗⊥]6 + \vec{a}\cdot\vec{c}_{\perp} = [\vec{a}, \vec{b}, \vec{c}_{\perp}]: 6+(−3)=[a⃗,b⃗,c⃗⊥]  ⟹  [a⃗,b⃗,c⃗⊥]=36 + (-3) = [\vec{a}, \vec{b}, \vec{c}_{\perp}] \implies [\vec{a}, \vec{b}, \vec{c}_{\perp}] = 3. Therefore, ∣[a⃗,c⃗,b⃗]∣=∣[a⃗,b⃗,c⃗]∣=∣[a⃗,b⃗,c⃗⊥]∣=∣3∣=3|[\vec{a}, \vec{c}, \vec{b}]| = |[\vec{a}, \vec{b}, \vec{c}]| = |[\vec{a}, \vec{b}, \vec{c}_{\perp}]| = |3| = 3.