Solveeit Logo
Login

Question

Question: If \(\vec{a},\vec{b},\vec{c}\) are the position vectors of the vertices of an equilateral triangle w...

If a⃗,b⃗,c⃗\vec{a},\vec{b},\vec{c} are the position vectors of the vertices of an equilateral triangle whose orthocenter is at the origin, then write the value of a⃗+b⃗+c⃗\vec{a}+\vec{b}+\vec{c}

Explanation

Solution

In problem we have given that the positional vectors of the vertices of an equilateral triangle. We know that the orthocenter of an equilateral triangle is at its centroid. So, using the positional vectors of the vertices we will find the centroid of the triangle. But in the problem, they mentioned that the orthocenter lies at the origin. So, we will equate the ortho center to the origin to get the result.

Complete step by step answer:
In the above problem they have mentioned the term Position Vectors. So first we will discuss what a Positional Vector is.
Positional Vector: The position vector is used to specify the position of a certain body. Knowing the position of a body is vital when it comes to describing the motion of that body. The position vector of an object is measured from the origin, in general. Suppose an object is placed in the space as shown:
Now the positional vector of the object at point AA is given by
r⃗=xi^+yj^+zk^\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}
Where
i^\hat{i} is the unit vector in the direction of x−axisx-axis
j^\hat{j} is the unit vector in the direction of y−axisy-axis
k^\hat{k} is the unit vector in the direction of z−axisz-axis
Given that,
a⃗,b⃗,c⃗\vec{a},\vec{b},\vec{c} are the position vectors of the vertices of an equilateral triangle, then the triangle is shown in below

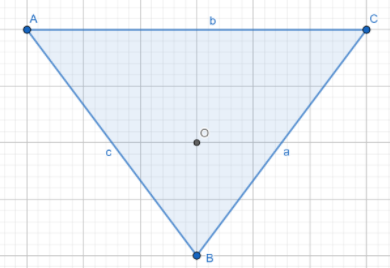
Here OO be the ortho center of the triangle. But in an equilateral triangle orthocenter lies at the centroid of the triangle. So, the centroid of the equilateral triangle with the positional vectors a⃗,b⃗,c⃗\vec{a},\vec{b},\vec{c} is given by
O=a⃗+b⃗+c⃗3O=\dfrac{\vec{a}+\vec{b}+\vec{c}}{3}
But in the problem, they mentioned that the orthocenter is at Origin. We know the position vector of the origin is O⃗=0i^+0j^+0k^\vec{O}=0\hat{i}+0\hat{j}+0\hat{k}
Hence
a⃗+b⃗+c⃗3=O⃗ a⃗+b⃗+c⃗=3(0i^+0j^+0k^) a⃗+b⃗+c⃗=0\begin{aligned} & \dfrac{\vec{a}+\vec{b}+\vec{c}}{3}=\vec{O} \\\ & \vec{a}+\vec{b}+\vec{c}=3\left( 0\hat{i}+0\hat{j}+0\hat{k} \right) \\\ & \vec{a}+\vec{b}+\vec{c}=0 \end{aligned}

So, the correct answer is “0”.

Note: Please understand the concept of vectors and difference between the positional vector and displacement vectors. Positional vector gives us the position of an object with respect to the origin. Whether the displacement vector gives the distance between the two positional vectors.