Question

If $\vec a,\vec b,\vec c$ and $\vec d$ are unit vectors such that $\left( {\vec a \times \vec b} \right) \cdot \left( {\vec c \times \vec d} \right) = 1$ and $\vec a \cdot \vec c = \dfrac{1}{2}$, then
A. $\vec a,\vec b,\vec c$ are non-coplanar
B. $\vec b,\vec c,\vec d$ are non-coplanar
C. $\vec b,\vec d$ are non-parallel
D. $\vec a,\vec d$ are parallel and $\vec b,\vec c$ are parallel

Answer 1

First of consider the angle between the vectors $\left( {\vec a \times \vec b} \right)$ and $\left( {\vec c \times \vec d} \right)$ as a variable and find its value to show that the two vectors are in parallel to each other. Likewise find the angle between the vectors $\vec a$ and $\vec c$. Then draw a figure for the vectors $\vec a,\vec b,\vec c$ and $\vec d$ to get the required answer.

Complete step-by-step answer:
Given that $\vec a,\vec b,\vec c$ and $\vec d$ are unit vectors. So, we have $\left| {\vec a} \right| = \left| {\vec b} \right| = \left| {\vec c} \right| = \left| {\vec d} \right| = 1$.
Also given that $\left( {\vec a \times \vec b} \right) \cdot \left( {\vec c \times \vec d} \right) = 1$
Let the angle between $\left( {\vec a \times \vec b} \right)$ and $\left( {\vec c \times \vec d} \right)$ be $\theta$.
We know that for the two vectors $\vec x$ and $\vec y$, the dot product is given by $\vec x \cdot \vec y = \left| {\vec x} \right|\left| {\vec y} \right|\cos \theta$ where $\theta$ is the angle between the two vectors $\vec x$ and $\vec y$.
By using this formula, we have

$$\Rightarrow \left( {\vec a \times \vec b} \right) \cdot \left( {\vec c \times \vec d} \right) = \left| {\vec a \times \vec b} \right|\left| {\vec c \times \vec d} \right|\cos \theta = 1 \\\ \Rightarrow \left| {\vec a \times \vec b} \right|\left| {\vec c \times \vec d} \right|\cos \theta = 1 \\\$$

This is only possible when $\left| {\vec a \times \vec b} \right| = \left| {\vec c \times \vec d} \right| = \cos \theta = 1$
So, we have $\cos \theta = 1$. Thus, $\theta = {90^0}$.
Since the angle between the vectors $\left( {\vec a \times \vec b} \right)$ and $\left( {\vec c \times \vec d} \right)$ is ${90^0}$ the two vectors $\left( {\vec a \times \vec b} \right)$ and $\left( {\vec c \times \vec d} \right)$ are parallel to each other i.e., $\left( {\vec a \times \vec b} \right)\parallel \left( {\vec c \times \vec d} \right)..................................\left( 1 \right)$
Also given that $\vec a \cdot \vec c = \dfrac{1}{2}$. Let the angle between the two vectors $\vec a,\vec c$ be $\alpha$. So, we have

$$\Rightarrow \left| {\vec a} \right|\left| {\vec c} \right|\cos \alpha = \dfrac{1}{2} \\\ \Rightarrow 1 \times 1 \times \cos \alpha = \dfrac{1}{2}{\text{ }}\left[ {\because \left| {\vec a} \right| = \left| {\vec c} \right| = 1} \right] \\\ \Rightarrow \cos \alpha = \dfrac{1}{2} \\\ \therefore \alpha = {60^0}{\text{ }}\left[ {\because \cos {{60}^0} = \dfrac{1}{2}} \right]{\text{ }} \\\$$

We can draw the vectors as

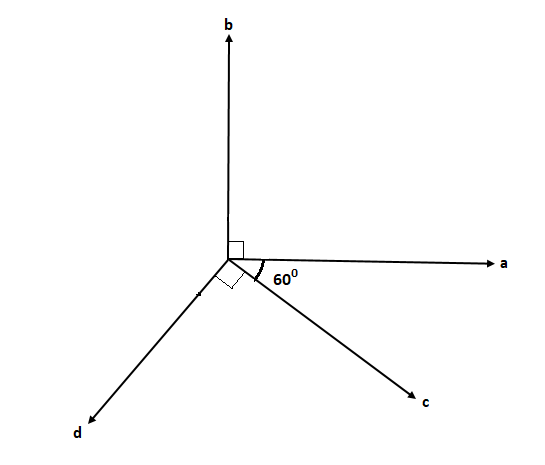
Since the two vectors $\left( {\vec a \times \vec b} \right)$ and $\left( {\vec c \times \vec d} \right)$ are parallel to each other and the angle between the vectors $\vec a$ and $\vec c$is ${60^0}$ we can say that $\vec b$ and $\vec d$ are not parallel.
Thus, the correct option is C. $\vec b,\vec d$ are non-parallel

So, the correct answer is “Option C”.

Note: For the two vectors $\vec x$ and $\vec y$, the dot product is given by $\vec x \cdot \vec y = \left| {\vec x} \right|\left| {\vec y} \right|\cos \theta$ where $\theta$ is the angle between the two vectors $\vec x$ and $\vec y$. And for the two vectors $\vec x$ and $\vec y$, the cross product is given by $\vec x \times \vec y = \left| {\vec x} \right|\left| {\vec y} \right|\sin \theta$ where $\theta$ is the angle between the two vectors $\vec x$ and $\vec y$.