Question

If ${{V}_{A}}$ and ${{V}_{B}}$ denote the potentials of A and B, then the equivalent resistance between A and B in the adjoint electric circuit is-

A). $10\Omega$ if ${{V}_{A}}>{{V}_{B}}$
B). $5\Omega$ if ${{V}_{A}}<{{V}_{B}}$
C). $5\Omega$ if ${{V}_{A}}>{{V}_{B}}$
D). $20\Omega$ if ${{V}_{A}}>{{V}_{B}}$

Answer 1

The diode will allow the current to pass only when it is forward biased. If the diode is not forward biased, then it will not allow current to flow through it. We will use this concept to solve the question.

Formula Used:
Resistances in series: ${{R}_{net}}={{R}_{1}}+{{R}_{2}}$
Resistances in parallel: ${{R}_{net}}=\dfrac{{{R}_{1}}{{R}_{2}}}{{{R}_{1}}+{{R}_{2}}}$

Complete step-by-step solution:
Here, there are various conditions given in the options. It basically boils down to whether ${{V}_{A}}>{{V}_{B}}$ or ${{V}_{A}}<{{V}_{B}}$.
We will apply these conditions to the circuits and see what is the behavior of the diode under these conditions.
Case-1: ${{V}_{A}}>{{V}_{B}}$:
Here, if we consider ${{V}_{A}}>{{V}_{B}}$, then we can say that the positive terminal of the diode is connected to the higher potential. This will make the diode forward biased and the diode will become a short circuit and will allow the current to flow through it. The diagram will be:

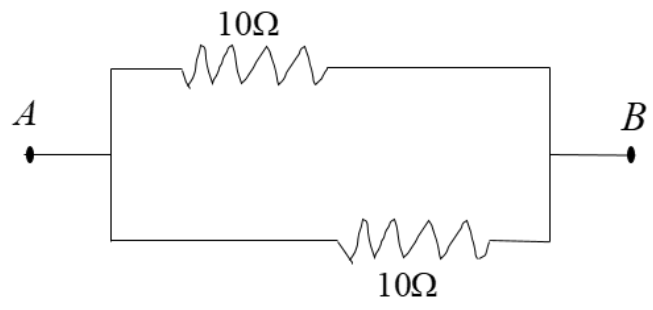
It can be seen clearly that the resistances $10\Omega$ and $10\Omega$ are in parallel. Hence, the net resistance between A and B will be:
${{R}_{AB}}=\dfrac{10\Omega }{2}=5\Omega$
Case-2: ${{V}_{A}}<{{V}_{B}}$:
In this case, the negative terminal of the diode is connected to the higher potential. This will make the diode reversed biased and the diode will become an open circuit. This will not allow any current to flow through the diode. The diagram will look like:

It can be seen clearly that the $10\Omega$ in the above branch becomes out of the circuit.
Hence, clearly, the resistance between A and B becomes:
${{R}_{AB}}=10\Omega$
Thus, ${{V}_{A}}>{{V}_{B}}$ $\Rightarrow {{R}_{AB}}=5\Omega$
& ${{V}_{A}}<{{V}_{B}}$ $\Rightarrow {{R}_{AB}}=10\Omega$
Thus clearly, the answer is an option (c).

Note: Forward biased diode acts as a short circuit in the branch. It allows current to easily flow through it. The reversed biased diode acts as an open circuit in the branch. It does not allow any current to flow through it.