Question

If two tangents to an ellipse and one of its foci be given, prove that the locus of its centre is a straight line.

Answer 1

Hint: Consider T as the tangent drawn to the ellipse. Use the equation to find the polar form of tangent. Take focus ‘S’ of the ellipse is (ae, 0) and for $s'$ $\left( -ae,0 \right)$. Find the polar form of Tangents to prove the locus of its centre is a straight line.

Complete step by step answer:
Let us consider $T$ as the tangent that is drawn to the ellipse. $TP$ and $TQ$ are the two tangents from $T$, which has their focus at $S.$ The focus $S$ of the ellipse is $\left( ae,0 \right)$ and for $S_1$ $\left( -ae,0 \right)$.
Hence we need to prove that $\angle QT{{S}_{1}}=\angle PTS$ ( from figure).

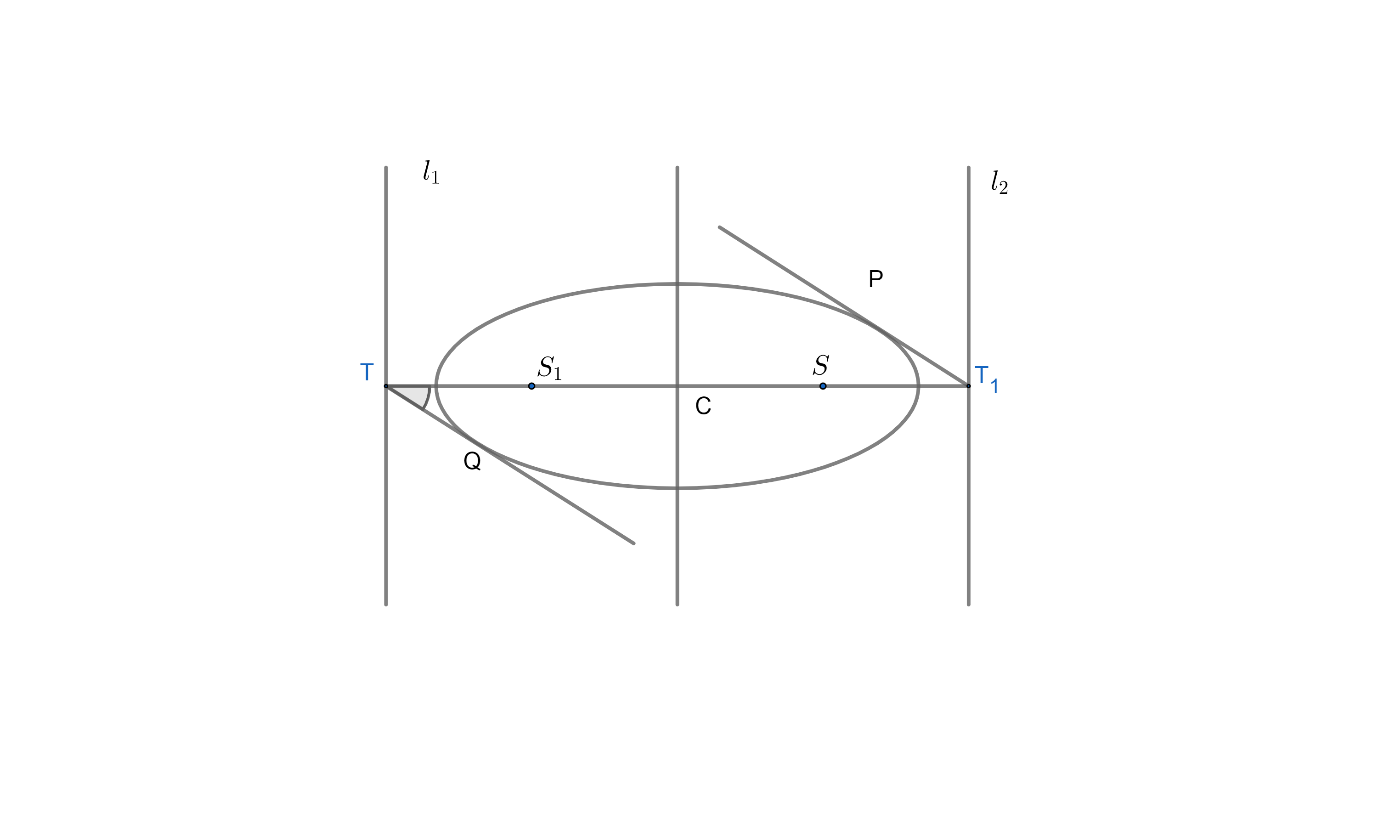
The centre $C$ of the ellipse is midway between S and ${{S}_{1}}$ , which are the focus.
Let the coordinate of any point be $\left( h,k \right)$ and equation to ellipse is
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1............\left( 1 \right)$
To find the polar form of tangent we have the equation $\dfrac{x{{x}_{1}}}{{{a}^{2}}}+\dfrac{y{{y}_{1}}}{{{b}^{2}}}=1..............\left( 2 \right)$
$\left( h,k \right)=\left( {{x}_{1}},{{y}_{1}} \right)$
$\therefore$ Substituting values in $\left( 2 \right)\Rightarrow \dfrac{xh}{{{a}^{2}}}+\dfrac{yk}{{{b}^{2}}}=1...........\left( 3 \right)$
By hypothesis $\Rightarrow \dfrac{1}{\sqrt{\dfrac{{{h}^{2}}}{{{a}^{2}}}+\dfrac{{{k}^{2}}}{{{b}^{2}}}}}=c$ is the length of perpendicular from centre $\left( 0,0 \right)$ is given this
On squaring and cross multiplying we get
$\dfrac{1}{2}=\dfrac{{{h}^{2}}}{{{a}^{4}}}+\dfrac{{{k}^{2}}}{{{b}^{4}}}$
Now generalizing the locus of $\left( h,k \right)$ , we get $\dfrac{{{x}^{2}}}{{{a}^{4}}}+\dfrac{{{y}^{2}}}{{{b}^{4}}}=\dfrac{1}{{{c}^{2}}}$

We got the locus of its centre, so when ${{S}_{1}}$ moves on $T{{S}_{1}}, C$ will move parallel to $T{{S}_{1}}$ so that they will bisect the line $S{{S}_{1}}$. Therefore we were able to prove that the locus of centre $C$ is a straight line.

Note: Remember that two tangents drawn from any point to an ellipse subtend equal angle at the focus.