Question

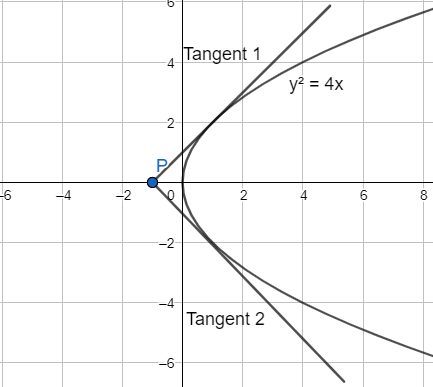
If two tangent draw from a point P to the parabola ${{y}^{2}}=4x$ are at right angles, then the locus of P is
a) $2x+1=0$
b) $x=-1$
c) $2x-1=0$
d) $x+1$

Answer 1

Hint: We can consider the equation of tangent as $y=mx+c$. We can then use the condition $c=\dfrac{a}{m}$ . Then, we can get two equations of tangents. To find the slope of tangent, we can divide them and using the condition for the slope of perpendicular lines, we can solve it further.

Complete step-by-step answer:
Let the given parabola be ${{y}^{2}}=4x$. Comparing with the standard equation of parabola ${{y}^{2}}=4ax$, we get $a=1$,

Equation of the tangent can be written in terms of slope m.
Let the equation of tangent to parabola is $y=mx+c$ …(1)
Where m is slope of tangent, c is intercept of line, and a is focal point of parabola.
We know the condition between tangents to a parabola is $c=\dfrac{a}{m}$ . Hence, the equation of tangent $y=mx+c$ can be written as $y=mx+\dfrac{a}{m}$ ; $a=1$. Let the given point P is (h,k).
Equation of tangent 1:
$y={{m}_{1}}x+\dfrac{1}{{{m}_{1}}}$ …(2)
${{m}_{1}}$ is the slope of tangent 1
Equation of tangent 2:
$y={{m}_{2}}x+\dfrac{1}{{{m}_{2}}}$ …(3)
${{m}_{2}}$is the slope of tangent 2
Now, we have the equation of both tangents in the terms of slope. Dividing equation (2) & (3), we get,
$\begin{aligned} & {{m}_{2}}x+\dfrac{1}{{{m}_{2}}}={{m}_{1}}x+\dfrac{1}{{{m}_{1}}} \\\ & x({{m}_{2}}-{{m}_{1}})=\dfrac{1}{{{m}_{1}}}-\dfrac{1}{{{m}_{2}}} \\\ & x({{m}_{2}}-{{m}_{1}})=\dfrac{{{m}_{2}}-{{m}_{1}}}{{{m}_{1}}{{m}_{2}}} \\\ & x=\dfrac{1}{{{m}_{1}}{{m}_{2}}} \\\ \end{aligned}$
It’s given that two tangents making right angles at point P. If two line are perpendicular with slope ${{m}_{1}}$ & ${{m}_{2}}$ respectively, then condition is ${{m}_{1}}{{m}_{2}}=-1$. So,
$\begin{aligned} & x=\dfrac{1}{{{m}_{1}}{{m}_{2}}} \\\ & x=-1 \\\ \end{aligned}$
Hence, correct option be (b)

Note: Use the relationship between tangent to parabola is $c=\dfrac{a}{m}$ to get the answer in the easiest way. And write the equation of tangent in the terms of the slope of the tangents as it was mentioned in the question that both tangents are perpendicular to each other. If we observe the figure carefully, we can see that the locus of point P is the directrix of the parabola. So, whenever we have a question with two tangents to parabola at right angles, we can verify by checking if we have got the final answer as the directrix. Directrix is given by $x=-a\Rightarrow x=-1$ .